题目内容
在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求
| BD | AC |
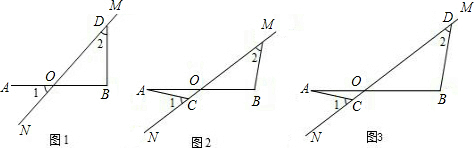
分析:(1)根据等腰直角三角形的判定和性质得出;
(2)过点B作BE∥CA交DO于E,通过证明△AOC≌△BOE,得出AC=BE,∠ACO=∠BEO,从而∠DEB=∠2,则BE=BD,等量代换得出AC=BD.延长AC交DB的延长线于F,根据平行线的性质及已知得出AC⊥BD;
(3)过点B作BE∥CA交DO于E,通过证明△BOE∽△AOC,根据相似三角形的性质得出
的值.
(2)过点B作BE∥CA交DO于E,通过证明△AOC≌△BOE,得出AC=BE,∠ACO=∠BEO,从而∠DEB=∠2,则BE=BD,等量代换得出AC=BD.延长AC交DB的延长线于F,根据平行线的性质及已知得出AC⊥BD;
(3)过点B作BE∥CA交DO于E,通过证明△BOE∽△AOC,根据相似三角形的性质得出
| BD |
| AC |
解答:(1)解:AO=BD,AO⊥BD;
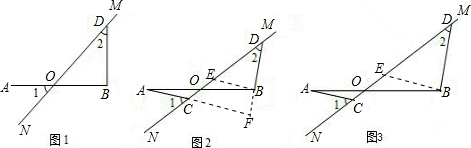
(2)证明:如图2,过点B作BE∥CA交DO于E,
则∠ACO=∠BEO.
又∵AO=OB,∠AOC=∠BOE,
∴△AOC≌△BOE.
∴AC=BE.
又∵∠1=45°,
∴∠ACO=∠BEO=135°.
∴∠DEB=45°.
∵∠2=45°,
∴BE=BD,∠EBD=90°.
∴AC=BD.
延长AC交DB的延长线于F,如图.
∵BE∥AC,
∴∠AFD=90°.
∴AC⊥BD.
(3)解:如图3,过点B作BE∥CA交DO于E,
则∠BEO=∠ACO.
又∵∠BOE=∠AOC,
∴△BOE∽△AOC.
∴
=
.
又∵OB=kAO,
由(2)的方法易得BE=BD.
∴
=k
答:
的值为k.

(2)证明:如图2,过点B作BE∥CA交DO于E,
则∠ACO=∠BEO.
又∵AO=OB,∠AOC=∠BOE,
∴△AOC≌△BOE.
∴AC=BE.
又∵∠1=45°,
∴∠ACO=∠BEO=135°.
∴∠DEB=45°.
∵∠2=45°,
∴BE=BD,∠EBD=90°.
∴AC=BD.
延长AC交DB的延长线于F,如图.
∵BE∥AC,
∴∠AFD=90°.
∴AC⊥BD.
(3)解:如图3,过点B作BE∥CA交DO于E,
则∠BEO=∠ACO.
又∵∠BOE=∠AOC,
∴△BOE∽△AOC.
∴
| BE |
| AC |
| BO |
| AO |
又∵OB=kAO,
由(2)的方法易得BE=BD.
∴
| BD |
| AC |
答:
| BD |
| AC |
点评:本题主要考查了等腰直角三角形的判定和性质,平行线的性质及相似三角形的判定和性质,综合性强,难度较大.
另外还可以过A作AA’垂直AC于A这样好像简单些!
另外还可以过A作AA’垂直AC于A这样好像简单些!

练习册系列答案
相关题目
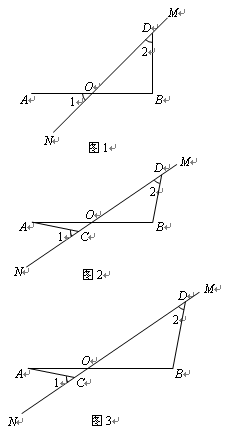
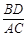 的值.
的值.
 的值.
的值.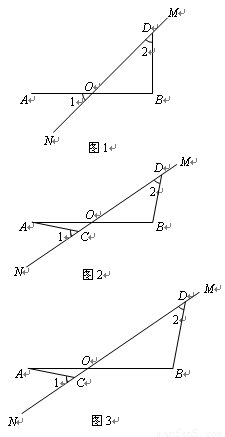
 的值.
的值.
