题目内容
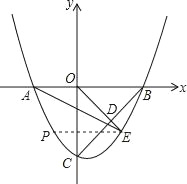
【题目】如图,对称轴为直线x=![]() 的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
的抛物线与y轴交于点C(0,﹣3),与x轴交于A、B两点(点A在点B的左侧),AB=5
(1)求A、B两点的坐标及该抛物线对应的解析式;
(2)D为BC的中点,延长OD与抛物线在第四象限内交于点E,连结AE、BE.
①求点E的坐标;
②判断ABE的形状,并说明理由;
(3)在x轴下方的抛物线上,是否存在一点P,使得四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)①E(2,﹣2),②△ABE是直角三角形;(3)存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).
x﹣3;(2)①E(2,﹣2),②△ABE是直角三角形;(3)存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).
【解析】试题分析:
(1)由抛物线的对称轴为直线![]() ,与
,与![]() 轴交于A、B两点(点A在点B的左侧),AB=5,可得点A、B的坐标分别为(﹣2,0),B(3,0),由此可设抛物线解析式为:
轴交于A、B两点(点A在点B的左侧),AB=5,可得点A、B的坐标分别为(﹣2,0),B(3,0),由此可设抛物线解析式为: ![]() ,再代入点C(0,-3)解出
,再代入点C(0,-3)解出![]() 的值即可求得解析式;
的值即可求得解析式;
(2)①根据线段中点坐标公式由点B、C的坐标可得点D的坐标,由点D的坐标可求得直线OD的解析式;解有OD的解析式和抛物线的解析式组成的方程组即可得到点E的坐标;
②由点A、B、E的坐标可求出AB、BE、AE的长度,根据勾股定理逆定理可判断出△ABE是直角三角形;
(3)过点E作EP∥OB交抛物线于点P,根据点P和E关于直线![]() 对称,求得点P的坐标,进一步可求得PE的长,若PE=OB,则点P符合要求,否则就不存在符合要求的点P.
对称,求得点P的坐标,进一步可求得PE的长,若PE=OB,则点P符合要求,否则就不存在符合要求的点P.
试题解析:
(1)∵点A、B关于对称轴![]() 对称,且AB=5
对称,且AB=5
∴A(﹣2,0),B(3,0),
∴可设抛物线的解析式为: ![]() ,
,
把点C的坐标(0,﹣3)代入得: ![]() ,解得:
,解得: ![]() ,
,
∴该二次函数的解析式为: ![]() ,即
,即![]() ;
;
(2)①∵点B、C的坐标分别为:(3,0),(0,﹣3),
∴线段BC的中点D的坐标为: ![]() .
.
设直线OE的解析式为: ![]() ,
,
把 D![]() ,代入
,代入![]() 解得:
解得: ![]() ,
,
∴OE的解析式为: ![]() ,
,
由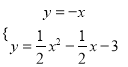 ,解得
,解得![]() ,
, ![]() ,
,
又因为点E在第四象限,
∴E的坐标为(2,﹣2).
②∵AE=![]() ,BE=
,BE=![]() ,AB=5,
,AB=5,
∴AB2=AE2+BE2,
∴△ABE是直角三角形;
(3)存在满足条件的点P
过E作PE∥OB,交抛物线于点P,
∵点P和点E(2,﹣2)关于对称轴![]() 对称
对称
∴P的坐标为(﹣1,﹣2),
∴PE=3=OB,
又∵PE∥OB,
∴四边形OBEP是平行四边形,
∴存在点P,使四边形OBEP是平行四边形,坐标为(﹣1,﹣2).

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案