题目内容
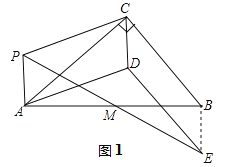
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;

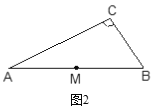
(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
【答案】(1)见解析;(2)DE//BC;DE=BC;(3)DE⊥AC;(4)M(1,1)或(-1,-1)或(9,5).
【解析】
(1)根据图1的构图条件,在Rt△ABC内的任取一点P,作图即可;
(2)连接BE,根据边角边可证△PAM和△EBM全等,可得EB和PA既平行又相等,而PA和CD既平行且相等,所以DE和BC平行相等,
(3)由(2)得BC⊥AC,DE∥BC,所以DE也和AC垂直;
(4)以A、C、D、M为点构造成平行四边形的顶点顺序没定,故有三种情况:分别过点A,C,D作线段CD,AD,AC的平行线,三条直线的交点即为能以A、C、D、M为点构造成平行四边形的点M的位置,再利用平行四边形的性质及平移知识即可求得点M 的坐标
解:(1)作图如图2:
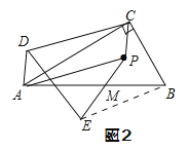
(2)观察图1,图2,猜想线段DE和线段BC数量和位置关系为:DE=BC,DE//BC;
选择图1,证明如下:
连接BE,
∵PM=ME,∠PMA=∠EMB,AM=MB,
∴△PMA≌△EMB.(SAS)
∵PA=BE,∠MPA=∠MEB,
∴PA∥BE.
∵平行四边形PADC,
∴PA∥DC,PA=DC.
∴BE∥DC,BE=DC,
∴四边形DEBC是平行四边形.
∴DE∥BC,DE=BC.
(3)猜想DE⊥AC;理由如下:
∵∠ACB=90°,
∴BC⊥AC,
又∵DE∥BC,(已证)
∴DE⊥AC.
(3)如图3
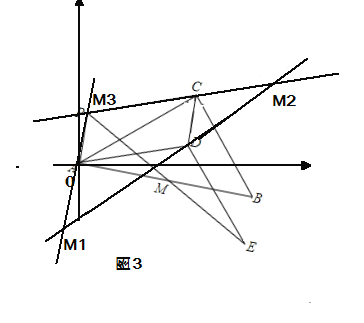
分别过点A,C,D作线段CD,AD,AC的平行线,三条直线分别相交于点![]() ,则得到
,则得到![]() 即为满足条件的点M,使以A、C、D、M为点构造成平行四边形.理由如下:
即为满足条件的点M,使以A、C、D、M为点构造成平行四边形.理由如下:
∵AC//DM1,CD//AM1,
∴四边形ACDM1为平行四边形,
同理可得:四边形ACM2D为平行四边形,四边形ADCM3为平行四边形.
设M1的坐标为(x,y),
由于四边形ACDM1为平行四边形,
∴AC//M1D,AC=M1D.可以看做线段AC经过适当的平移到线段M1D.
C与D为对应点,A与M1为对应点,
易知:点C(5,3)向左平移一个单位,向下平移一个单位得到D(4,2).
故点A也向左平移一个单位,向下平移一个单位得到M1(x,y),即
0-1=x,0-1=y,所以x=-1,y=-1.点M1的坐标为(-1,-1),同理可得
M2的坐标为(9,5),M3的坐标为(1,1).
故存在M点,分别为(1,1)或(-1,-1)或(9,5).使以A、C、D、M为点构造成平行四边形

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案