题目内容
已知: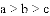
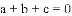
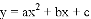 的图象可能是下列图象中的( )
的图象可能是下列图象中的( )
A. 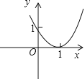 B.
B. 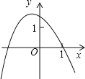 C.
C. 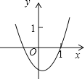 D.
D. 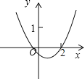
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
抛物线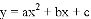 上部分点的横坐标
上部分点的横坐标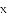

| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与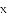
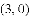
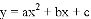 的最大值为
的最大值为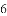
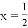 ;④在对称轴左侧,
;④在对称轴左侧,
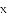
A. 0个 B. 1个 C. 2个 D. 3个
题目内容
已知: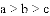
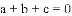
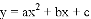 的图象可能是下列图象中的( )
的图象可能是下列图象中的( )
A.  B.
B.  C.
C.  D.
D. 
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案抛物线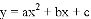 上部分点的横坐标
上部分点的横坐标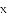

| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表,得出下面结论:①抛物线与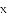
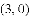
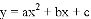 的最大值为
的最大值为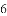
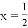 ;④在对称轴左侧,
;④在对称轴左侧,
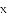
A. 0个 B. 1个 C. 2个 D. 3个