题目内容
已知:⊙O的半径OA=5,弦AB=8,C是弦AB的中点,点P是射线AO上一点(与点A不重合),直线PC与射线BO交于点D.(1)当点P在⊙O上,求OD的长.
(2)若点P在AO的延长线上,设OP=x,
 ,求y与x的函数关系式并写出自变量x的取值范围.
,求y与x的函数关系式并写出自变量x的取值范围.(3)连接CO,若△PCO与△PCA相似,求此时BD的长.

【答案】分析:(1)连接BP,根据C是AB的中点,O是AP的中点,判断出点D是△ABP的重心,然后根据三角形的重心到顶点的距离等于对边中点的距离的2倍解答即可;
(2)过点O作OE∥AB,交PC于点E,根据平行线分线段成比例定理表示出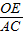 、
、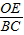 ,再根据点C是AB的中点整理即可得解;
,再根据点C是AB的中点整理即可得解;
(3)①当P在AO延长线上时,根据相似三角形对应角相等可得∠PCO=∠A,然后求出∠PCO=∠ABO,再根据等腰三角形三线合一的性质可得OC⊥AB,然后求出∠AOC=∠BCD,再求出△ACO和△BDC相似,然后根据相似三角形对应边成比例列式求解即可;②P在AO上时,根据△PCO与△PCA相似先判定出CP⊥AO,利用相似三角形对应边成比例列式求出PO,过点B作BH⊥AO于H,再求出OH,然后利用相似三角形对应边成比例列式求出OD,再根据BD=OB+OD代入数据计算即可得解.
解答: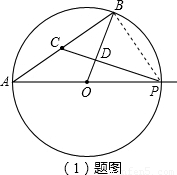 解:(1)当P在⊙O上时,连接BP,
解:(1)当P在⊙O上时,连接BP,
∵C是AB中点,O是AP中点,
∴点D为△ABP的重心,
∴OD= OB,
OB,
∵OA=OB=5,
∴OD= ×5=
×5= ;
;
(2)如图,过点O作OE∥AB,交PC于点E,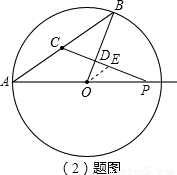
∵OE∥AB,
∴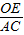 =
=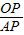 ,
,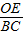 =
=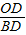 ,
,
又∵AC=BC,
∴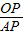 =
=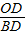 ,
,
即y=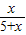 (x>0);
(x>0);
(3)①如图1,当P在AO延长线上时,
∵△PCO∽△PAC,
∴∠PCO=∠A,
∵∠A=∠ABO,
∴∠PCO=∠ABO,
∵OA=OB,点C是AB的中点,
∴OC⊥AB,
∴∠PCO+∠BCD=90°,
又∵∠A+∠AOC=90°,
∴∠BCD=∠AOC,
∴△ACO∽△BDC,
∴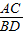 =
=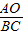 ,
,
即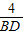 =
= ,
,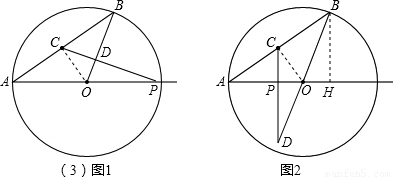
∴BD=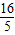 ;
;
②如图2,当P在AO上时,∵△PCO∽△PAC,
∴∠PCO=∠A,
∴∠A+∠ACP=∠PCO+∠ACP=90°,
∴CP⊥AO,
∴△ACP∽△AOC,
∴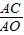 =
=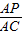 ,
,
∵AB=8,C是AB的中点,
∴AC= ×8=4,
×8=4,
∴ =
=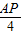 ,
,
解得AP=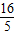 ,
,
∴PO=AO-AP=5-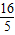 =
= ,
,
过点B作BH⊥AO于H,则OH=PH-OP=AP-OP=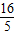 -
- =
= ,
,
∵CP⊥AO,BH⊥AO,
∴PD∥BH,
∴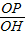 =
=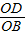 ,
,
即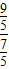 =
=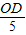 ,
,
∴OD=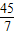 ,
,
∴BD=OB+OD=5+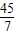 =
=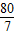 ,
,
综上所述,若△PCO与△PCA相似,此时BD的长为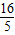 或
或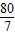 .
.
点评:本题是圆的综合题型,主要考查了三角形的重心性质,平行线分线段成比例定理,相似三角形的判定与性质,(1)需要熟记三角形的重心到顶点的距离等于对边中点的距离的2倍,(2)作辅助线利用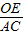 =
=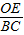 起到中间过渡是解题的关键,(3)难点在于要分情况讨论.
起到中间过渡是解题的关键,(3)难点在于要分情况讨论.
(2)过点O作OE∥AB,交PC于点E,根据平行线分线段成比例定理表示出
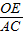 、
、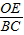 ,再根据点C是AB的中点整理即可得解;
,再根据点C是AB的中点整理即可得解;(3)①当P在AO延长线上时,根据相似三角形对应角相等可得∠PCO=∠A,然后求出∠PCO=∠ABO,再根据等腰三角形三线合一的性质可得OC⊥AB,然后求出∠AOC=∠BCD,再求出△ACO和△BDC相似,然后根据相似三角形对应边成比例列式求解即可;②P在AO上时,根据△PCO与△PCA相似先判定出CP⊥AO,利用相似三角形对应边成比例列式求出PO,过点B作BH⊥AO于H,再求出OH,然后利用相似三角形对应边成比例列式求出OD,再根据BD=OB+OD代入数据计算即可得解.
解答:
 解:(1)当P在⊙O上时,连接BP,
解:(1)当P在⊙O上时,连接BP,∵C是AB中点,O是AP中点,
∴点D为△ABP的重心,
∴OD=
 OB,
OB,∵OA=OB=5,
∴OD=
 ×5=
×5= ;
;(2)如图,过点O作OE∥AB,交PC于点E,

∵OE∥AB,
∴
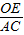 =
=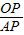 ,
,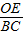 =
=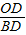 ,
,又∵AC=BC,
∴
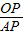 =
=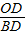 ,
,即y=
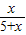 (x>0);
(x>0);(3)①如图1,当P在AO延长线上时,
∵△PCO∽△PAC,
∴∠PCO=∠A,
∵∠A=∠ABO,
∴∠PCO=∠ABO,
∵OA=OB,点C是AB的中点,
∴OC⊥AB,
∴∠PCO+∠BCD=90°,
又∵∠A+∠AOC=90°,
∴∠BCD=∠AOC,
∴△ACO∽△BDC,
∴
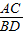 =
=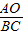 ,
,即
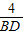 =
= ,
,
∴BD=
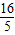 ;
;②如图2,当P在AO上时,∵△PCO∽△PAC,
∴∠PCO=∠A,
∴∠A+∠ACP=∠PCO+∠ACP=90°,
∴CP⊥AO,
∴△ACP∽△AOC,
∴
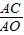 =
=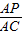 ,
,∵AB=8,C是AB的中点,
∴AC=
 ×8=4,
×8=4,∴
 =
=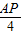 ,
,解得AP=
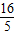 ,
,∴PO=AO-AP=5-
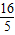 =
= ,
,过点B作BH⊥AO于H,则OH=PH-OP=AP-OP=
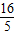 -
- =
= ,
,∵CP⊥AO,BH⊥AO,
∴PD∥BH,
∴
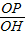 =
=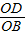 ,
,即
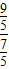 =
=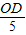 ,
,∴OD=
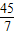 ,
,∴BD=OB+OD=5+
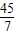 =
=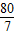 ,
,综上所述,若△PCO与△PCA相似,此时BD的长为
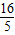 或
或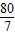 .
.点评:本题是圆的综合题型,主要考查了三角形的重心性质,平行线分线段成比例定理,相似三角形的判定与性质,(1)需要熟记三角形的重心到顶点的距离等于对边中点的距离的2倍,(2)作辅助线利用
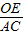 =
=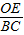 起到中间过渡是解题的关键,(3)难点在于要分情况讨论.
起到中间过渡是解题的关键,(3)难点在于要分情况讨论. 
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为
如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为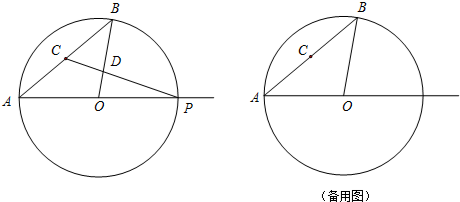
 如图,已知大圆的半径OA=6cm,且AB⊥CD,则图中阴影部分的面积是
如图,已知大圆的半径OA=6cm,且AB⊥CD,则图中阴影部分的面积是

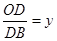 ,求y与x的函数关系式并写出自变量x 的取值范围。
,求y与x的函数关系式并写出自变量x 的取值范围。