Question

【题目】已知：在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（5，4），B（0，3），C（2，1）．

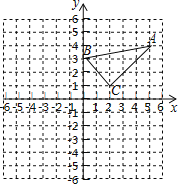
（1）画出△ABC关于原点成中心对称的△A1B1C1，并写出点C1的坐标；

（2）画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）分别找出点A、B、C关于原点的对称点A1、B1、C1，然后连接A1B1，B1C1，A1C1即可，然后根据关于原点对称的两点坐标规律：横、纵坐标均互为相反数即可求出点C1的坐标；

（2）分别将线段B1C1，A1C1绕点C1按顺时针旋转90°，得出B2C1，A2C1，然后连接B2A2即可．

（1）分别找出点A、B、C关于原点的对称点A1、B1、C1，然后连接A1B1，B1C1，A1C1，如图所示，△A1B1C1即为所求，

∵C（2，1）

∴点C1的坐标为（﹣2，﹣1）．

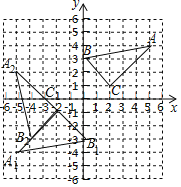
（2）分别将线段B1C1，A1C1绕点C1按顺时针旋转90°，得出B2C1，A2C1，然后连接B2A2，如图所示，△A2B2C1即为所求．