题目内容
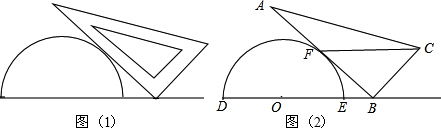
将一个量角器和一个含30°角的直角三角板如图1放置,图2是由它抽象出的几何图形,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,BC=OD(1)求证:FC∥DB;
(2)当OD=3,sin∠ABD=
| 3 | 5 |
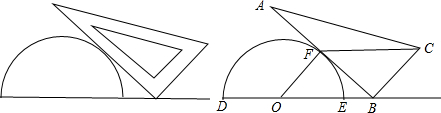
分析:(1)由AB切半圆O于点F,得到∠OFB=90°,而∠ABC=90°,则OF∥BC,而OF=OD=BC,得到四边形OFCB是平行四边形,所以FC∥DB;
(2)在Rt△OFB中,根据sin∠ABO=
,OF=OD=3,得到OB=5,FB=4.在Rt△ABC中,得到AB=3
,即可得到AF的长.
(2)在Rt△OFB中,根据sin∠ABO=
| 3 |
| 5 |
| 3 |
解答:(1)证明:∵AB切半圆O于点F,
∴OF⊥AB,
即∠OFB=90°,
又∵△ABC为直角三角形,
∴∠ABC=90°.
∴∠OFB=∠ABC.
∴OF∥BC.
又∵OF=OD,OD=BC,
∴OF=BC.
∴四边形OFCB是平行四边形.
∴FC∥OB.
即FC∥DB;
(2)解:在Rt△OFB中,
∵sin∠ABO=
,OF=OD=3,
∴OB=5,FB=4.
在Rt△ABC中,
∵∠ABC=90°,∠A=30°,BC=OD=3,
∴AB=3
.
∴AF=3
-4.
∴OF⊥AB,
即∠OFB=90°,
又∵△ABC为直角三角形,
∴∠ABC=90°.
∴∠OFB=∠ABC.
∴OF∥BC.
又∵OF=OD,OD=BC,
∴OF=BC.
∴四边形OFCB是平行四边形.
∴FC∥OB.
即FC∥DB;
(2)解:在Rt△OFB中,
∵sin∠ABO=
| 3 |
| 5 |
∴OB=5,FB=4.
在Rt△ABC中,
∵∠ABC=90°,∠A=30°,BC=OD=3,
∴AB=3
| 3 |
∴AF=3
| 3 |
点评:本题考查了切线的性质:圆心与切点的连线垂直切线;过圆心垂直于切线的直线必过切点;过圆外一点引圆的两条切线,切线长相等.也考查了平行四边形的判定与性质以及含30度角的直角三角形三边的关系.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目



 的长度。
的长度。 