题目内容
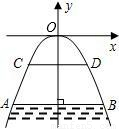
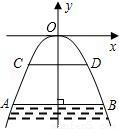
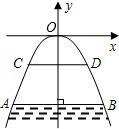 如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.(1)在如图的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
分析:先设抛物线的解析式,再找出几个点的坐标,代入解析式后可求解.
解答:解:(1)设所求抛物线的解析式为:y=ax2(a≠0),
由CD=10m,可设D(5,b),
由AB=20m,水位上升3m就达到警戒线CD,
则B(10,b-3),
把D、B的坐标分别代入y=ax2得:
,
解得
.
∴y=-
x2;
(2)∵b=-1,
∴拱桥顶O到CD的距离为1m,
∴
=5(小时).
所以再持续5小时到达拱桥顶.
由CD=10m,可设D(5,b),
由AB=20m,水位上升3m就达到警戒线CD,
则B(10,b-3),
把D、B的坐标分别代入y=ax2得:
|
解得
|
∴y=-
| 1 |
| 25 |
(2)∵b=-1,
∴拱桥顶O到CD的距离为1m,
∴
| 1 |
| 0.2 |
所以再持续5小时到达拱桥顶.
点评:命题立意:此题是把一个实际问题通过数学建模,转化为二次函数问题,用二次函数的性质加以解决.

练习册系列答案
相关题目