Question

【题目】将正三角形、正四边形、正五边形按如图所示的位置摆放．如果∠3=30°，那么∠1+∠2=°．

Answer 1

【答案】72
【解析】解：如图 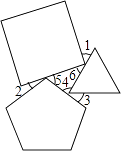， ∵∠3=30°，正三角形的内角是60°，正四边形的内角是90°，正五边形的内角是108°，
∴∠4=180°﹣60°﹣30°=90°，
∴∠5+∠6=180°﹣80°=90°，
∴∠5=180°﹣∠2﹣108° ①，
∠6=180°﹣90°﹣∠1=90°﹣∠1 ②，
∴①+②得，180°﹣∠2﹣108°+90°﹣∠1=90°，
即∠1+∠2=72°．
所以答案是：72．
【考点精析】通过灵活运用等边三角形的性质和多边形内角与外角，掌握等边三角形的三个角都相等并且每个角都是60°；多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°即可以解答此题．