题目内容
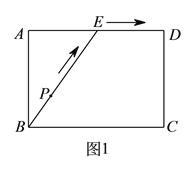
【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=![]() (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D.
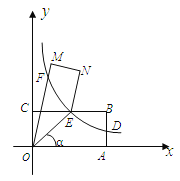
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=![]() 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
形OMNE除点E外的另一个交点为F,求直线DF的解析式
【答案】(1)见解析 (2)① a=2b ②![]()
【解析】分析:(1)根据中点坐标公式得到E点坐标,再根据待定系数法得到双曲线解析式,把D点的横坐标代入可求D点的纵坐标,依此即可证明;
(2)①根据等腰直角三角形的性质即可得到a、b之间的数量关系;
②首先过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,由∠EOA=30°,k=![]() ,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
详解: ![]() ,
,
![]() ,
,
![]() ,得:
,得:![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() (3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
(3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
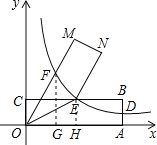
∵∠AOE=30°,k=![]() ,
,
∴![]() =
=![]() ,
,
∴OH=![]() EH,
EH,
∵S△EOH=![]() OHEH=
OHEH=![]() k=
k=![]() ,
,
∴EH=1,OH=![]() ,
,
∵E是BC的中点,
∴OA=2OH=2![]() ,
,
∴点D的横坐标为2![]() ,
,
则y=![]() ,
,
∴点D(2![]() ,
,![]() ),
),
由折叠的性质可得:∠FOA=2∠AOE=60°,
∴FG:OG=![]() ,
,
∵S△FOG=![]() OGFG=
OGFG=![]() k═
k═![]() ,
,
∴OG=1,FG=![]() ,
,
∴点F(1,![]() ),
),
设直线EF的解析式为:y=ax+b,
则 ,
,
解得: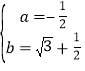 ,
,
∴直线EF的解析式为:y=![]() x+
x+![]() +
+![]() .
.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减情况 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?