题目内容
五一假期将至,电器市场将火爆.根据市场调查,某商店需进某种电视机和洗衣机,决定电视机的进货量不少于洗衣机进货量的一半,电视机与洗衣机的进价、售价如下表:
现计划进电视机和洗衣机共100台,商店最多可凑资金270000元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价外费用)
(2)哪种进货方案待商店销售完进的电视机与洗衣机后获得利润最大?并求出最大利润.
| | 电视机 | 洗衣机 |
| 进价(元/台) | 3200 | 2400 |
| 售价(元/台) | 3800 | 2900 |
现计划进电视机和洗衣机共100台,商店最多可凑资金270000元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价外费用)
(2)哪种进货方案待商店销售完进的电视机与洗衣机后获得利润最大?并求出最大利润.
(1)设进电视机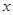 台,则洗衣机
台,则洗衣机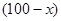 台
台
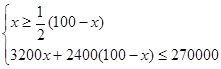 解得
解得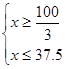
所以
 ,所以共4种方案:电视机37台,洗衣机63台;电视机38台,洗衣机62台;电视机39台,洗衣机61台;电视机40台,洗衣机60台. ……………………4分
,所以共4种方案:电视机37台,洗衣机63台;电视机38台,洗衣机62台;电视机39台,洗衣机61台;电视机40台,洗衣机60台. ……………………4分
(2)总利润为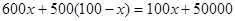
因为总利润随着x的增大而增大,所以当x=37时,总利润最大为53700元…8分
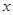 台,则洗衣机
台,则洗衣机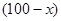 台
台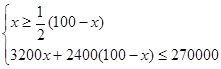 解得
解得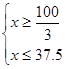
所以

 ,所以共4种方案:电视机37台,洗衣机63台;电视机38台,洗衣机62台;电视机39台,洗衣机61台;电视机40台,洗衣机60台. ……………………4分
,所以共4种方案:电视机37台,洗衣机63台;电视机38台,洗衣机62台;电视机39台,洗衣机61台;电视机40台,洗衣机60台. ……………………4分(2)总利润为
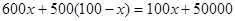
因为总利润随着x的增大而增大,所以当x=37时,总利润最大为53700元…8分
(1)设购进电视x台,洗衣机就为(100-x)台,根据电视机的进价为3200元/台,洗衣机的进价为2400元/台,根据电视机进货量不少于洗衣机的进货量的一半,以及超市最多可筹集资金270000元可列不等式组求解.
(2)列得利润关于x的一次函数关系式,根据一次函数x的系数大于0,得到此一次函数为增函数,把第一问中x的最大值代入函数解析式求出的值为利润的最大值,.
(2)列得利润关于x的一次函数关系式,根据一次函数x的系数大于0,得到此一次函数为增函数,把第一问中x的最大值代入函数解析式求出的值为利润的最大值,.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 外安全区,若导火线燃烧的速度为
外安全区,若导火线燃烧的速度为 /s,人跑步的速度为
/s,人跑步的速度为 /s,则导火线的长应大于 cm.
/s,则导火线的长应大于 cm.
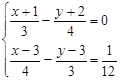
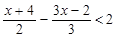
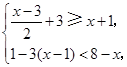 (在数轴上表示解集并写出符合的整数解)
(在数轴上表示解集并写出符合的整数解) <
< <1时,点P(
<1时,点P( )在 象限。
)在 象限。

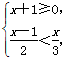 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.