题目内容
【题目】我们都知道“三角形的内角和等于180°”。如图1,教材中是用“延长BC,过点C作CE∥AB”的方法把∠A移到∠1的位置,把∠B移到∠2的位置,从而完成证明的。请你借助图2作辅助线的思路将下面证明“三角形的内角和等于180°”的过程补充完整。
已知:△ABC
求证:∠BAC+∠B+∠C=180°
证明:如图2,过点A作直线DE∥BC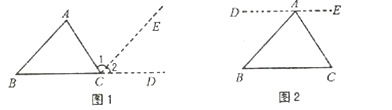
【答案】解:∵DE∥BC
∴∠B=∠DAB ∠C=∠EAC ,
∴∠BAC+∠B+∠C=∠BAC+∠DAB+∠EAC=180° ,
∴∠BAC+∠B+∠C=180° 。
【解析】根据二直线平行内错角相等得出∠B=∠DAB ∠C=∠EAC ,根据平角的定义及等量代换得出∠BAC+∠B+∠C=∠BAC+∠DAB+∠EAC=180° 。

练习册系列答案
相关题目
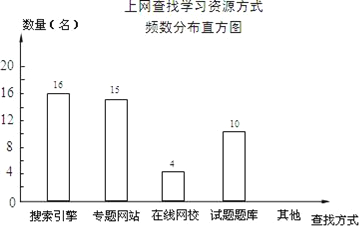
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a= ;b= ;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?