题目内容
已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上.
求证:AE、AF把∠BAC三等分.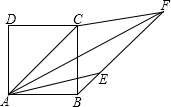
求证:AE、AF把∠BAC三等分.


证明:如图,连接BD,交AC于点O,作EG⊥AC,垂足为G点,
∵四边形AEFC为菱形,
∴EF∥AC.
∴GE=OB,
∵四边形ABCD为正方形,
∴OB⊥AC,
∴OB∥GE,
∵AE=AC,OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=
| 1 |
| 2 |
∴∠EAG=30°.
∴∠BAE=15°.
在菱形AEFC中,AF平分∠EAC,
∴∠EAF=∠FAC=
| 1 |
| 2 |
∴∠EAB=∠FAE=∠FAC.
即AE、AF把∠BAC三等分.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 7、已知,如图,以正方形ABCD的一边BC向正方形内作等边△EBC,则∠ABE=
7、已知,如图,以正方形ABCD的一边BC向正方形内作等边△EBC,则∠ABE= 已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上.
已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上. 已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上.
已知:如图,以正方形ABCD的对角线为边作菱形AEFC,B在FE的延长线上.