题目内容
菱形一条对角线长为8m，周长为20m，则其面积为（ ）
| A、40m2 |
| B、20m2 |
| C、48m2 |
| D、24m2 |
考点：菱形的性质
专题：几何图形问题
分析：菱形对角线互相垂直平分，所以OA2+OB2=AB2，根据已知可得AB=5，BO=4，利用勾股定理求得AO，即可求得AC的长，根据AC、BD即可求菱形ABCD的面积，即可解题．
解答：解：根据题意可得：BD=8m，则BO=DO=4m，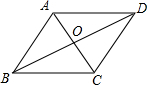
∵菱形周长为20m，
∴AB=5m，
∵菱形对角线互相垂直平分，
∴OA2+OB2=AB2，
∴AO=
=3（m），
∴AC=6（m），
故菱形的面积S=
×6×8=24（m2）．
故选D．．
∵菱形周长为20m，
∴AB=5m，
∵菱形对角线互相垂直平分，
∴OA2+OB2=AB2，
∴AO=
| AB2-OB2 |
∴AC=6（m），
故菱形的面积S=
| 1 |
| 2 |
故选D．．
点评：本题考查了菱形对角线互相垂直平分的性质，菱形面积的计算，本题中根据勾股定理求AO的值是解题的关键．
练习册系列答案
相关题目
如图所示，BF、DE相交于点A，BG交BF于点B，交AC于点C．已知关于x的不等式组
无解，则a的取值范围是（ ）
|
| A、a≤-1 |
| B、a≤2 |
| C、-1＜a＜2 |
| D、a＜-1或a＞2 |
已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（ ）
| A、AD平分∠BAC |
| B、AB=AC且BD=CD |
| C、AD为中线 |
| D、EF⊥AD |
要使式子
有意义，字母x的取值范围为（ ）
| 2x-3 |
| A、x≥0 | ||
| B、x＞1 | ||
C、x≥
| ||
D、x≥
|
