题目内容
已知锐角A满足关系式2sin2A-5sinA+2=0，则sinA的值为
- A.
或2 - B.2
- C.
- D.以上都不对
C
分析：首先把方程左边分解因式得：（2sinA-1）（sinA-2）=0，再变为一元一次方程，即可解出sinA的值．
解答：2sin2A-5sinA+2=0，
把方程左边分解因式得：（2sinA-1）（sinA-2）=0，
2sinA-1=0，sinA-2=0，
解得：sinA=或2（不合题意舍去），
故选：C．
点评：此题主要考查了因式分解法解一元二次方程，关键是正确把方程的左边分解因式．
分析：首先把方程左边分解因式得：（2sinA-1）（sinA-2）=0，再变为一元一次方程，即可解出sinA的值．
解答：2sin2A-5sinA+2=0，
把方程左边分解因式得：（2sinA-1）（sinA-2）=0，
2sinA-1=0，sinA-2=0，
解得：sinA=
或2（不合题意舍去），故选：C．
点评：此题主要考查了因式分解法解一元二次方程，关键是正确把方程的左边分解因式．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
已知锐角A满足关系式2sin2A-7sinA+3=0，则sinA的值为（ ）
A、
| ||
| B、3 | ||
C、
| ||
| D、4 |
已知锐角A满足关系式2cos2A-7cosA+3=0，则cosA的值为（ ）
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
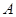满足关系式
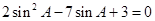，则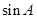
的值为（ ）
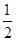B．3 C．