Question

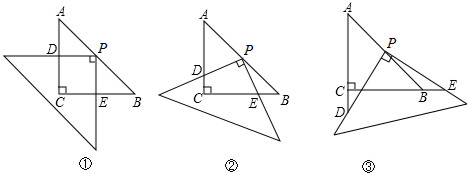
操作：在△ABC中，AC=BC=4，∠C=90°，将一块直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．如图①、②、③是旋转三角板得到的图形中的3种情况．

探究：（1）如图①，PD⊥AC于D，PE⊥BC于E，则重叠部分四边形DCEP的面积为

4

，周长

8

．
（2）三角板绕点P旋转，观察线段PD与PE之间有什么数量关系？并结合图②加以证明．
（3）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由．

Answer 1

分析：（1）根据点P是AB的中点可判断出PD、PE是△ABC的中位线，继而可得出PD、PE的长度，也可得出四边形DCEP的周长和面积．
（2）先根据图形可猜测PD=PE，从而连接CP，通过证明△PCD≌△PEB，可得出结论．
（3）题目只要求是等腰三角形，所以需要分三种情况进行讨论，这样每一种情况下的CE的长也就不难得出．

解答：解：（1）根据△ABC中，AC=BC=4，∠C=90°，
∵PD⊥AC，PE⊥BC，
∴PD∥BC，PE∥AC，
又∵点P是AB中点，
∴PD、PE是△ABC的中位线，
∴PD=CE=2，PE=CD=2，
∴四边形DCEP是正方形，面积为2×2=4，周长为2+2+2+4=8；

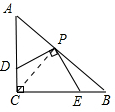（2）证明如下，AC=BC，∠C=90°，P为AB中点，连接CP，
∴CP平分∠C，CP⊥AB，
∵∠PCB=∠B=45°，
∴CP=PB，
∵∠DPC+∠CPE=∠CPE+∠EPB=90°，
∴∠DPC=∠EPB，
在△PCD和△PEB中，

∠DPC=∠EPB CP=PB ∠DCP=∠B

，
∴△PCD≌△PBE（ASA），
∴PD=PE．

（3）△PBE是等腰三角形，
①当PE=PB时，此时点C与点E重合，CE=0；
②1）当PB=BE时，E在线段BC上，CE=2-

2

，2）E在CB的延长线上，CE=2+

2

；
③当PE=BE时，CE=1．

点评：本题考查了旋转的性质、等腰三角形的性质与判定，第三问的解答应分情况进行论证，不能漏解，有一定难度．