题目内容
如果△ABC中,sinA=cosB= ,则下列最确切的结论是
,则下列最确切的结论是
- A.△ABC是直角三角形
- B.△ABC是等腰三角形
- C.△ABC是等腰直角三角形
- D.△ABC是锐角三角形
C
分析:根据特殊角的三角函数值,直接得出∠A,∠B的角度从而得出答案.
解答:∵sinA=cosB= ,
,
∴∠A=∠B=45°,
∴△ABC是等腰直角三角形.
故选C.
点评:此题主要考查了特殊角的三角函数值,正确的记忆特殊角的三角函数值是解决问题的关键.
分析:根据特殊角的三角函数值,直接得出∠A,∠B的角度从而得出答案.
解答:∵sinA=cosB=
 ,
,∴∠A=∠B=45°,
∴△ABC是等腰直角三角形.
故选C.
点评:此题主要考查了特殊角的三角函数值,正确的记忆特殊角的三角函数值是解决问题的关键.

练习册系列答案
相关题目
如果△ABC中,sinA=cosB=
,则下列最确切的结论是( )
| ||
| 2 |
| A、△ABC是直角三角形 |
| B、△ABC是等腰三角形 |
| C、△ABC是等腰直角三角形 |
| D、△ABC是锐角三角形 |
如果△ABC中,sinA=cosB=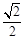 ,则下列最确切的结论是( )
,则下列最确切的结论是( )
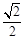 ,则下列最确切的结论是( )
,则下列最确切的结论是( )| A.△ABC是直角三角形 | B.△ABC是等腰三角形 |
| C.△ABC是等腰直角三角形 | D.△ABC是锐角三角形 |
 ,则下列最确切的结论是(
)
,则下列最确切的结论是(
)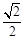 ,则下列最确切的结论是(
)
,则下列最确切的结论是(
)