题目内容
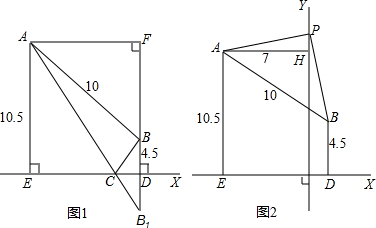
我区的自然风光无限,最具特色的是青龙大峡谷(A)和文佛奇峰山(B),它们位于笔直的高速公路X同侧,AB=10km,A,B到直线X的距离分别为AE=10.5km和BD=4.5km.(1)方案一:旅游开发公司计划在高速公路X旁修建一服务区C,并从服务区C向A、B两景区修建笔直公路运送游客.公司选择较节省的方案(如图1:点B关于直线X的对称点是B1,连接AB1交直线X于点C),C到A、B的距离之和S1=AC+BC,求S1.
(2)方案二:在A,B两景区之间有一条与高速公路X垂直的省级公路Y,且A到省级公路Y的距离AH=7km(如图2).旅游开发公司打算在省级公路Y旁修建一服务区P,并从服务区P向A、B两景区修建笔直公路运送游客.由于地形条件的限制,P只能选择图2的位置,通过测量得PA=PB,P到A、B的距离之和S2=AP+BP.请你通过计算比较S1,S2的大小.(参考数据:
| 2 |
分析:(1)先根据勾股定理求出BF的长,再利用点B关于直线X的对称点是B1,求证△AEC∽△CDB1,利用相似三角形对应变成比例求出EC和CD,然后利用勾股定理分别求出AC、BC即可.
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,利用轴对称-最短线路问题求出BM,设PH=x,根据勾股定理和已知条件AP=BP列出方程,求出PH,然后即可求得AP,从而可以比较比较S1,S2的大小.
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,利用轴对称-最短线路问题求出BM,设PH=x,根据勾股定理和已知条件AP=BP列出方程,求出PH,然后即可求得AP,从而可以比较比较S1,S2的大小.
解答:解:由笔直的高速公路X同侧,AB=10km,A,B到直线X的距离分别为AE=10.5km和BD=4.5km.知,BF=DF-BD=10.5-4.5=6,
∴AF=
=
=8,
∵点B关于直线X的对称点是B1,
∴BB1⊥CD,∴BD=DB1,
∴
=
,
∴
=
,
∴EC=5.6,
则CD=BD-EC=8-5.6=2.4,
AC=
=
=11.9,
BC=
=
=5.1,
S1=AC+BC=11.9+5.1=17km,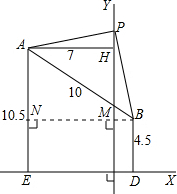
答:(1)S1=17km;
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,
∵Y⊥X,∴AN=HM=10.5-4.5=6,
∵ED=8(已求出),AH=7(已知),
∴BM=BN-NM=ED-AH=8-7=1,
设PH=x,则PM=HM+PH=6+x,
在Rt△AHP中,AP2=AH2+PH2,
在Rt△PBM中,BP2=PM2+MB2,
又∵AP=BP,
∴72+x2=(x+6)2+12,
解得x=1,则AP=
=
=5
,
S2=2AP=10
=14.14.
∵10
<17,
∴S1>S2.
∴AF=
| AB2-BF2 |
| 100-36 |
∵点B关于直线X的对称点是B1,
∴BB1⊥CD,∴BD=DB1,
∴
| AE |
| DB1 |
| EC |
| CD |
∴
| 10.5 |
| 4.5 |
| EC |
| 8-EC |
∴EC=5.6,
则CD=BD-EC=8-5.6=2.4,
AC=
| AE2+EC2 |
| 10.52+5.62 |
BC=
| CD2+BD2 |
| 2.42+4.52 |
S1=AC+BC=11.9+5.1=17km,

答:(1)S1=17km;
(2)过B点作BN⊥AE,交公路Y于M,交AE于N,
∵Y⊥X,∴AN=HM=10.5-4.5=6,
∵ED=8(已求出),AH=7(已知),
∴BM=BN-NM=ED-AH=8-7=1,
设PH=x,则PM=HM+PH=6+x,
在Rt△AHP中,AP2=AH2+PH2,
在Rt△PBM中,BP2=PM2+MB2,
又∵AP=BP,
∴72+x2=(x+6)2+12,
解得x=1,则AP=
| AH2+PH2 |
| 49+1 |
| 2 |
S2=2AP=10
| 2 |
∵10
| 2 |
∴S1>S2.
点评:此题主要考查学生对轴对称-最短线路问题和勾股定理的应用等知识点.步骤繁琐有一定的拔高难度,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )
)