题目内容
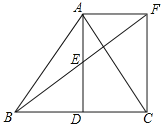
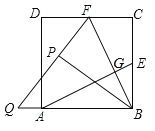
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:
①AE=BF;②S四边形ECFG=S△ABG;③△BFQ是等腰三角形;④![]() .
.
其中一定正确的个数是( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①根据正方形的性质和已知条件证明△ABE≌△BCF即可;②根据三角形ABE和三角形BFC面积相等即可证明S四边形ECFG=S△ABG;③根据折叠可得∠CFB=∠PFB,由DC∥AB得∠CFB=∠FBA,等量代换后即可证明△BFQ是等腰三角形;④可以设正方形边长为1,AQ=x,AH=y,作FI⊥AB于点I,进而根据同角三角函数值相等用含x的式子表示y,然后求出QH,利用勾股定理列出方程求出x的值,即可得到![]() .
.
解:①∵在正方形ABCD中,E、F分别为BC、CD的中点,
∴AB=BC,∠ABE=∠BCF=90°,BE=CF,
∴△ABE≌△BCF(SAS),
∴AE=BF,故①正确;
②∵△ABE≌△BCF,
∴S△BCF=S△ABE,
∴SBCF﹣S△BGE=S△ABE﹣S△BGE,即S四边形ECFG=S△ABG,故②正确;
③∵由折叠可知:∠CFB=∠PFB,
∵DC∥AB,
∴∠CFB=∠FBA,
∴∠PFB=∠FBA,
∴QF=QB,
∴△BFQ是等腰三角形,故③正确;
④如图所示:
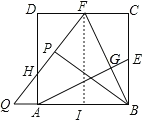
设PQ与AD交于点H,作FI⊥AB于点I,则四边形DAIF是矩形,
设正方形ABCD边长为1,AQ=x,AH=y,
则FI=AD=1,AI=![]() ,QI=x+
,QI=x+![]() ,
,
在Rt△AQH和Rt△FIQ中,tan∠Q=![]() ,即
,即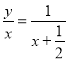 ,
,
∴y=![]() ,
,
∵AH∥FI,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△AHQ中,根据勾股定理得:x2+y2=y2(1+x)2,
∴x2+(![]() )2=(
)2=(![]() )2(1+x)2,
)2(1+x)2,
解得:x=![]() ,
,
经检验,x=![]() 是方程的解,
是方程的解,
∴BQ![]() ,
,
∴![]() ,故④正确.
,故④正确.
∴正确的是①②③④,
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案