题目内容
已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=-1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当-1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
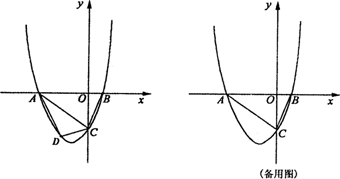
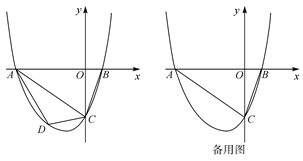
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
答案:
解析:
解析:
|
解:(Ⅰ)当 方程 ∴该抛物线与 (Ⅱ)当 对于方程 ①当 此时抛物线为 ②当 由已知 应有 解得 综上, (Ⅲ)对于二次函数 由已知 又 于是 ∴ ∵关于 ∴抛物线 又该抛物线的对称轴 由 得 ∴ 又由已知 可知在
|

练习册系列答案
相关题目
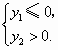 即
即