题目内容
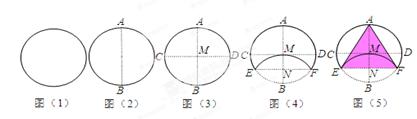
将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。

(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥ 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥
 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
(1)(0,5);(2)∠1=∠2.∵EG∥x轴,∴∠1=∠3. ∴∠2=∠3.∴EH=CH.
(3)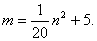 (4)
(4)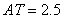 .
.
(3)
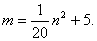 (4)
(4)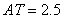 .
.试题分析:
(1) 当点O落在D点时候,则CD=OC=10.在Rt△DBC时,
BD=
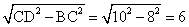 所以AD=AB-BD=10-6=4.设OE=x。则ED=x。AE=8-x、
所以AD=AB-BD=10-6=4.设OE=x。则ED=x。AE=8-x、则
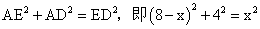 。解得x=5.所以点E坐标(0,5);
。解得x=5.所以点E坐标(0,5);(2)证明:(如图②)
由题意可知∠1=∠2.
∵EG∥x轴,∴∠1=∠3. ∴∠2=∠3.
∴EH=CH.
(3)
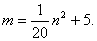
(4)解:(如图③)连接ET,
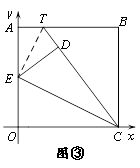
由题意可知,ED=EO,ED⊥TC,DC=OC=10,
∵E是AO中点,∴AE=EO.
∴AE=ED.
在Rt△ATE和Rt△DTE中,
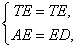
∴Rt△ATE≌Rt△DTE(HL).
∴AT=DT.
设
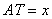 ,则
,则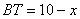 ,
,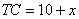 ,
,在Rt△BTC中,
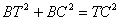 ,
,即
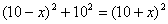 ,
,解得
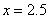 ,即
,即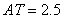 .
.点评:本题难度中等,主要考查学生对折叠性质结合几何性质等知识点综合运用能力。为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


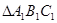 ,再将
,再将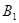 顺时针旋转90°得到
顺时针旋转90°得到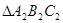 。
。
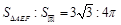 ,以上结论正确的有( )
,以上结论正确的有( )