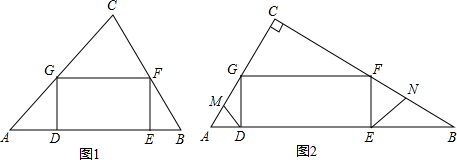
题目内容
在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F、G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若∠ACB=90°,如图2,线段DM、EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)直接写出矩形DEFG的面积的最大值.
注:在解本题时,可能要用到以下知识点,如果需要可直接引用结论.三角形内角角平分线定理:在△ABC中,当AD是顶角A的平分线交底边BC于D时,
=
.

(1)若AB=8,DE=2EF,求GF的长;
(2)若∠ACB=90°,如图2,线段DM、EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)直接写出矩形DEFG的面积的最大值.
注:在解本题时,可能要用到以下知识点,如果需要可直接引用结论.三角形内角角平分线定理:在△ABC中,当AD是顶角A的平分线交底边BC于D时,
| BD |
| CD |
| AB |
| AC |

分析:(1)根据三角形的面积公式即可求得△ABC的高,然后依据△CGF∽△CAB,相似三角形的对应边上的高的比等于相似比即可求得;
(2)过G作BC的平行线,过D作EN的平行线,两平行线交于P点.在DM上截取GQ=GP,连接QG,则△GPD≌△FNE,然后证明△GPD≌△GQD,根据等角对等边证明GM=GQ,从而证得结论;
(3)作CM⊥AB于M,交GF于点N.设BC=a,BC边上的高是h,DG=y,则CM=h,CN=h-y,ah=48,设GF=x,依据相似三角形的性质可以表示出矩形DEFG的面积,然后利用二次函数的性质即可求解.
(2)过G作BC的平行线,过D作EN的平行线,两平行线交于P点.在DM上截取GQ=GP,连接QG,则△GPD≌△FNE,然后证明△GPD≌△GQD,根据等角对等边证明GM=GQ,从而证得结论;
(3)作CM⊥AB于M,交GF于点N.设BC=a,BC边上的高是h,DG=y,则CM=h,CN=h-y,ah=48,设GF=x,依据相似三角形的性质可以表示出矩形DEFG的面积,然后利用二次函数的性质即可求解.
解答:解:(1)∵△ABC的面积是24,AB=8,
∴△ABC的高为6,
设GF=x,
∵矩形GDEF,DE=2EF,
∴GF∥DE,EF=
GF=
x,
∴△CGF∽△CAB,
∴
=
,
∴
=
,
∴x=4.8,
∴GF=4.8;
(2)过G作BC的平行线,过D作EN的平行线,两平行线交于P点,在DM上截取GQ=GP,连接QG,则△GPD≌△FNE,
∴FN=GP,
∵∠GDQ=∠GDP=45°,
∴△GPD≌△GQD.
∴GQ=GP,∠GQD=∠GPD,
∵∠MGP=∠MDP=90°,
∴∠GMD+∠GPD=180°,
∵∠GQM+∠GQD=180°,
∴∠GMQ=∠GQM,
∴GM=GQ,
∴MG=NF;
(3)作CM⊥AB于M,交GF于点N.
设BC=a,BC边上的高是h,DG=y,则CM=h,CN=h-y,ah=48,设GF=x.
∵△CGF∽△CAB,
∴
=
,即
=
,
则xh=ah-ay,
则y=
=
,
则矩形DEFG的面积s=xy=
•x,
即:S=-
x2+
x,
当x=
=
时,S有最大值,
最大值是:-
(
)2+
•
=-
+
=-
+
=12;
故矩形DEFG的面积的最大值是12.
∴△ABC的高为6,
设GF=x,
∵矩形GDEF,DE=2EF,
∴GF∥DE,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△CGF∽△CAB,
∴
| GF |
| AB |
| 6-EF |
| 6 |
∴
| x |
| 8 |
6-
| ||
| 6 |
∴x=4.8,
∴GF=4.8;
(2)过G作BC的平行线,过D作EN的平行线,两平行线交于P点,在DM上截取GQ=GP,连接QG,则△GPD≌△FNE,
∴FN=GP,

∵∠GDQ=∠GDP=45°,
∴△GPD≌△GQD.
∴GQ=GP,∠GQD=∠GPD,
∵∠MGP=∠MDP=90°,
∴∠GMD+∠GPD=180°,
∵∠GQM+∠GQD=180°,
∴∠GMQ=∠GQM,
∴GM=GQ,
∴MG=NF;
(3)作CM⊥AB于M,交GF于点N.

设BC=a,BC边上的高是h,DG=y,则CM=h,CN=h-y,ah=48,设GF=x.
∵△CGF∽△CAB,
∴
| GF |
| AB |
| h-EF |
| h |
| x |
| a |
| h-y |
| h |
则xh=ah-ay,
则y=
| ah-ay |
| a |
| 48-xh |
| a |
则矩形DEFG的面积s=xy=
| 48-xh |
| a |
即:S=-
| h |
| a |
| 48 |
| a |
当x=
| ||
-
|
| 24 |
| h |
最大值是:-
| h |
| a |
| 24 |
| h |
| 48 |
| a |
| 24 |
| h |
| 576 |
| ah |
| 48×24 |
| ah |
| 576 |
| 48 |
| 1152 |
| 48 |
故矩形DEFG的面积的最大值是12.
点评:此题考查了相似形的综合,用到的知识点是相似三角形的性质,二次函数的性质以及全等三角形的判定的综合应用,正确理解二次函数的性质是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
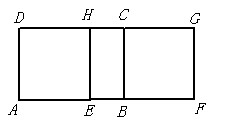 21、如图,在长方形ABCD中,AB=10cm,BC=6cm,若此长方形以2cm/S的速度沿着A→B方向移动,则经过多长时间,平移后的长方形与原来长方形重叠部分的面积为24?
21、如图,在长方形ABCD中,AB=10cm,BC=6cm,若此长方形以2cm/S的速度沿着A→B方向移动,则经过多长时间,平移后的长方形与原来长方形重叠部分的面积为24?