题目内容
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.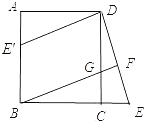
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
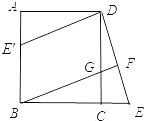
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.
【解析】(1)首先依据正方形的性质得到:BC=CD,∠BCD=∠DCE=90°,然后再依据SAS可证明△BCG≌△DCE;
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,然后依据等式的性质可证明BE′=DG,最后依据一组对边平行且相等的四边形是平行四边形可证明四边形E′BGD为平行四边形.
【考点精析】本题主要考查了平行四边形的判定和正方形的性质的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.