题目内容
 如图,抛物线
如图,抛物线 与直线AB交于点A(-1,0),B(4,
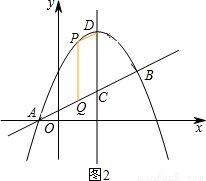
与直线AB交于点A(-1,0),B(4, ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;
(3)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】分析:(1)把点A、B的坐标分别代入函数解析式列出关于a、b的方程组,通过解方程组即可求得系数a、b的值;
(2)如图1,过点B作BF⊥DE于点F.则S= CD•(AE+BF)=-
CD•(AE+BF)=- (m-
(m- )2+
)2+ ,所以当m=
,所以当m= 时,S取最大值
时,S取最大值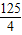 ;
;
(3)需要分类讨论:①如图2,当PQ∥DC,PQ=DC时.②如图3,当CD∥PQ,且CD=PQ时.③如图4,当PC∥DQ,且PC=DQ时.
分别求得这三种情况下的点Q的坐标.
解答: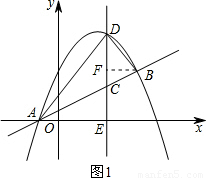 解:(1)∵抛物线
解:(1)∵抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).
).
∴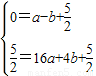 ,
,
解得,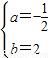 ,
,
∴抛物线的解析式是y=- x2+2x+
x2+2x+
(2)如图1,过点B作BF⊥DE于点F.
∵点A(-1,0),B(4, ),
),
∴易求直线AB的解析式为:y= x+
x+ .
.
又∵点D的横坐标为m,
∴点C的坐标是(m, m+
m+ ),点D的纵坐标是(-
),点D的纵坐标是(- m2+2m+
m2+2m+ )
)
∴AE=m+1,BF=4-m,CD=- m2+
m2+ m+2,
m+2,
∴S= CD•(AE+BF)=
CD•(AE+BF)= ×(-
×(- m2+
m2+ m+2)×(m+1+4-m)=-
m+2)×(m+1+4-m)=- (m-
(m- )2+
)2+ (-1<m<4).
(-1<m<4).
∴当m= 时,S取最大值
时,S取最大值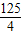 ,此时C(
,此时C( ,
, );
);
(3)假设存在这样的点P、Q使以点P,Q,C,D为顶点的四边形为平行四边形.
∵点D是抛物线的顶点,
∴D(2, ),C(2,
),C(2, ).
).
①如图2,当PQ∥DC,PQ=DC时.
设P(x,- x2+2x+
x2+2x+ ),则Q(x,
),则Q(x, x+
x+ ),
),
∴- x2+2x+
x2+2x+ -
- x-
x- =3,
=3,
解得,x=1或x=2(舍去),
∴Q(1,1);
②如图3,当CD∥PQ,且CD=PQ时.
设P(x,- x2+2x+
x2+2x+ ),则Q(x,
),则Q(x, x+
x+ ),
),
∴ x+
x+ +
+ x2-2x-
x2-2x- =3,
=3,
解得,x=5或x=-2,
∴Q(5,3)、Q′(-2,- );
);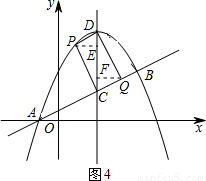
③如图4,当PC∥DQ,且PC=DQ时.
过点P作PE⊥CD于点E,过点Q作QF⊥CD于点F.则PE=QF,DE=FC.
设P(x,- x2+2x+
x2+2x+ ),则E(2,-
),则E(2,- x2+2x+
x2+2x+ ),
),
∴Q(4-x, -
- x),F(2,
x),F(2, -
- x),
x),
∴由DE=CF得, -(-
-(- x2+2x+
x2+2x+ )=
)= -
- x-
x- ,
,
解得,x=1或x=2(舍去),
∴Q(3,2)
综上所述,符合条件的点Q的坐标有:(1,1)、(5,3)、(-2,- )、(3,2).
)、(3,2).
点评:本题考查了二次函数综合题.其中涉及到的知识点有待定系数法求二次函数的解析式,抛物线的性质以及最值的求解方法.解答(3)题时要分类讨论.
(2)如图1,过点B作BF⊥DE于点F.则S=
 CD•(AE+BF)=-
CD•(AE+BF)=- (m-
(m- )2+
)2+ ,所以当m=
,所以当m= 时,S取最大值
时,S取最大值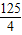 ;
;(3)需要分类讨论:①如图2,当PQ∥DC,PQ=DC时.②如图3,当CD∥PQ,且CD=PQ时.③如图4,当PC∥DQ,且PC=DQ时.
分别求得这三种情况下的点Q的坐标.
解答:
 解:(1)∵抛物线
解:(1)∵抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4, ).
).∴
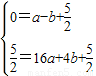 ,
,解得,
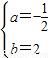 ,
,∴抛物线的解析式是y=-
 x2+2x+
x2+2x+
(2)如图1,过点B作BF⊥DE于点F.
∵点A(-1,0),B(4,
 ),
),∴易求直线AB的解析式为:y=
 x+
x+ .
.
又∵点D的横坐标为m,
∴点C的坐标是(m,
 m+
m+ ),点D的纵坐标是(-
),点D的纵坐标是(- m2+2m+
m2+2m+ )
)∴AE=m+1,BF=4-m,CD=-
 m2+
m2+ m+2,
m+2,∴S=
 CD•(AE+BF)=
CD•(AE+BF)= ×(-
×(- m2+
m2+ m+2)×(m+1+4-m)=-
m+2)×(m+1+4-m)=- (m-
(m- )2+
)2+ (-1<m<4).
(-1<m<4).∴当m=
 时,S取最大值
时,S取最大值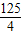 ,此时C(
,此时C( ,
, );
);(3)假设存在这样的点P、Q使以点P,Q,C,D为顶点的四边形为平行四边形.
∵点D是抛物线的顶点,
∴D(2,
 ),C(2,
),C(2, ).
).
①如图2,当PQ∥DC,PQ=DC时.
设P(x,-
 x2+2x+
x2+2x+ ),则Q(x,
),则Q(x, x+
x+ ),
),∴-
 x2+2x+
x2+2x+ -
- x-
x- =3,
=3,解得,x=1或x=2(舍去),
∴Q(1,1);
②如图3,当CD∥PQ,且CD=PQ时.
设P(x,-
 x2+2x+
x2+2x+ ),则Q(x,
),则Q(x, x+
x+ ),
),∴
 x+
x+ +
+ x2-2x-
x2-2x- =3,
=3,解得,x=5或x=-2,
∴Q(5,3)、Q′(-2,-
 );
);
③如图4,当PC∥DQ,且PC=DQ时.
过点P作PE⊥CD于点E,过点Q作QF⊥CD于点F.则PE=QF,DE=FC.
设P(x,-
 x2+2x+
x2+2x+ ),则E(2,-
),则E(2,- x2+2x+
x2+2x+ ),
),∴Q(4-x,
 -
- x),F(2,
x),F(2, -
- x),
x),∴由DE=CF得,
 -(-
-(- x2+2x+
x2+2x+ )=
)= -
- x-
x- ,
,解得,x=1或x=2(舍去),
∴Q(3,2)
综上所述,符合条件的点Q的坐标有:(1,1)、(5,3)、(-2,-
 )、(3,2).
)、(3,2).点评:本题考查了二次函数综合题.其中涉及到的知识点有待定系数法求二次函数的解析式,抛物线的性质以及最值的求解方法.解答(3)题时要分类讨论.

练习册系列答案
相关题目
 =-1,与x轴交于点C,且∠ABC=90°
=-1,与x轴交于点C,且∠ABC=90°
 与直线AB
与直线AB 交于x轴上的一点A,和另一点B(4,n).点P是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线PQ与直线AB垂直,交直线AB于点Q.
交于x轴上的一点A,和另一点B(4,n).点P是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线PQ与直线AB垂直,交直线AB于点Q.
 用含
用含 与直线
与直线 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为 。点P是y轴右侧的抛物线上一动点,过点P作
。点P是y轴右侧的抛物线上一动点,过点P作 轴于点E,交CD于点F.
轴于点E,交CD于点F.
 ,请直接写出相应的点P的坐标
,请直接写出相应的点P的坐标