题目内容
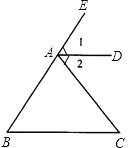
 23、(1)如图,把推理的根据填在括号内:
23、(1)如图,把推理的根据填在括号内:因为∠1=∠B(已知)
所以AD∥BC(
同位角相等,两直线平行
)所以∠C=∠2(
两直线平行,内错角相等
)因为∠B=∠C(已知)
所以∠1=∠2(等量代换)
所以AD是∠CAE的平分线(
角平分线的定义
)(2)灯塔B在灯塔A的北偏东60°,相距40海里,轮船在灯塔A的正东方向,在灯塔B的南偏东30°,试画图确定轮船C的位置.
分析:(1)根据平行线的判定及性质解答;
(2)根据题意画出方位图然后求解.
(2)根据题意画出方位图然后求解.
解答: 解:(1)∵∠1=∠B(已知),
解:(1)∵∠1=∠B(已知),
∴AD∥BC( 同位角相等,两直线平行),
∴∠C=∠2( 两直线平行,内错角相等);
∵∠B=∠C(已知),
∴∠1=∠2(等量代换),
∴AD是∠CAE的平分线( 角平分线定义).
(2)如图所示,按方位角的定义,根据题意,画出灯塔A的正东方向与灯塔B的南偏东30°方向的交点即可.
 解:(1)∵∠1=∠B(已知),
解:(1)∵∠1=∠B(已知),∴AD∥BC( 同位角相等,两直线平行),
∴∠C=∠2( 两直线平行,内错角相等);
∵∠B=∠C(已知),
∴∠1=∠2(等量代换),
∴AD是∠CAE的平分线( 角平分线定义).
(2)如图所示,按方位角的定义,根据题意,画出灯塔A的正东方向与灯塔B的南偏东30°方向的交点即可.
点评:此题的综合性较强,需要同学们熟练掌握平行线的性质以及判定.理解方位角的概念,并能灵活应用.

练习册系列答案
相关题目
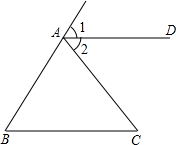 如图,把推理的根据填在括号内:
如图,把推理的根据填在括号内: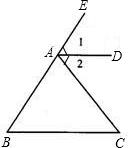 (1)如图,把推理的根据填在括号内:
(1)如图,把推理的根据填在括号内: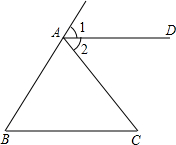 如图,把推理的根据填在括号内:
如图,把推理的根据填在括号内: