题目内容
线段AB上有任一点C,点E和点F分别是线段AC和线段CB的中点,若EF=4,则AB的长是( )
分析:根据题意,由E和点F分别是线段AC、CB的中点,即可而推出AC=2CE,BC=2CF,可知AB=AC+BC=2(CE+CF)=2EF,再由EF=5,即可推出AB的长度.
解答:解:∵点E和点F分别是线段AC和线段CB的中点,
∴AC=2CE,BC=2CF,
∵EF=4,
∴AB=AC+BC=2(CE+CF)=2EF=8.
故选:B.
∴AC=2CE,BC=2CF,
∵EF=4,
∴AB=AC+BC=2(CE+CF)=2EF=8.
故选:B.
点评:本题主要考查线段中点的性质,关键在于根据题意推出AB=AC+BC=2(CE+CF).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
线段AB上有任一点C,点E和点F分别是线段AC和线段CB的中点,若EF=4,则AB的长是( )。
| A.6 | B.8 | C.10 | D.12 |
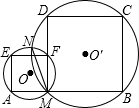
 2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )
2、已知,如图,线段AB上有任一点M,分别以AM,BM为边长作正方形AMFE、MBCD.正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点,则直线MN的情况是( )