题目内容
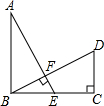 如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
如图所示,AB⊥BC,CD⊥BC,垂足分别为B、C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
- A.4cm
- B.8cm
- C.9cm
- D.10cm
B
分析:运用等角的余角相等,得出∠A=∠BFE,从而得到,△ABE≌△BCD,易求.
解答:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠ACD=90°
∴∠AEB+∠A=90°
∵AE⊥BD
∴∠BFE=90°
∴∠AEB+∠FBE=90°
∴∠A=∠BFE,
又∵AB=BC,
∴△ABE≌△BCD,
∴BE=CD=4cm,AB=BC
∵E为BC的中点
∴AB=BC=2BE=8cm.
故选B.
点评:本题综合运用了等角的余角相等,三角形全等的判定,性质等知识.需注意当题中出现两个或两个以上垂直时,一般要从中找到一对相等的角.
分析:运用等角的余角相等,得出∠A=∠BFE,从而得到,△ABE≌△BCD,易求.
解答:∵AB⊥BC,CD⊥BC,
∴∠ABC=∠ACD=90°
∴∠AEB+∠A=90°
∵AE⊥BD
∴∠BFE=90°
∴∠AEB+∠FBE=90°
∴∠A=∠BFE,
又∵AB=BC,
∴△ABE≌△BCD,
∴BE=CD=4cm,AB=BC
∵E为BC的中点
∴AB=BC=2BE=8cm.
故选B.
点评:本题综合运用了等角的余角相等,三角形全等的判定,性质等知识.需注意当题中出现两个或两个以上垂直时,一般要从中找到一对相等的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
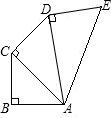 如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
 9、如图所示,AB⊥BC,DC⊥BC,E是BC上一点,∠BAE=∠DEC=60°,AB=3,CE=4,则AD等于( )
9、如图所示,AB⊥BC,DC⊥BC,E是BC上一点,∠BAE=∠DEC=60°,AB=3,CE=4,则AD等于( )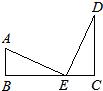 13、如图所示,AB⊥BC,DC⊥BC,若BE=CD,再增加条件
13、如图所示,AB⊥BC,DC⊥BC,若BE=CD,再增加条件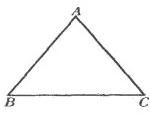
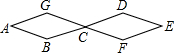 如图所示,AB=BC=CD=DE=EF=FC=CG=GA=1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序循环运动,行走2010厘米后停下,则这只蚂蚁停在
如图所示,AB=BC=CD=DE=EF=FC=CG=GA=1厘米,一只蚂蚁由A点开始按ABCDEFCGA的顺序循环运动,行走2010厘米后停下,则这只蚂蚁停在