题目内容
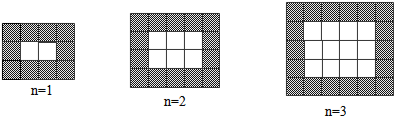
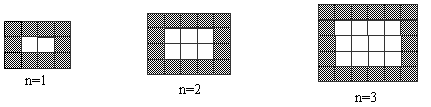
如图,用黑白两色正形瓷砖铺设矩形地面,请观察下图并解答有关问题:
(1)在第n个图中,每一横行共有______块瓷砖,每一竖列共有______块瓷砖,白色瓷砖共有______块;(用含n的代数式表示)
(2)设铺设地面所用瓷砖的总块数为y,请写出y与(1)中的n的关系式:______.

解:(1)在第n个图中,每一横行共有n+3块瓷砖,每一竖列共有n+2块瓷砖,白色瓷砖共有n(n+1)块;
(2)∵每一横行共有n+3块瓷砖,每一竖列共有n+2块瓷砖,
∴总块数y=(n+3)(n+2)(或y=n2+5n+6)
故答案为:n+3,n+2,n(n+1)(2)y=(n+3)(n+2)(或y=n2+5n+6)
分析:(1)仔细观察图形发现规律并利用规律解答即可.
(2)利用发现的横行瓷砖块数乘以竖行瓷砖块数即可求得总块数.
点评:本题考查图形的变化规律;得到每行和每列瓷砖的块数与图形序号的关系是解决本题的关键;
(2)∵每一横行共有n+3块瓷砖,每一竖列共有n+2块瓷砖,
∴总块数y=(n+3)(n+2)(或y=n2+5n+6)
故答案为:n+3,n+2,n(n+1)(2)y=(n+3)(n+2)(或y=n2+5n+6)
分析:(1)仔细观察图形发现规律并利用规律解答即可.
(2)利用发现的横行瓷砖块数乘以竖行瓷砖块数即可求得总块数.
点评:本题考查图形的变化规律;得到每行和每列瓷砖的块数与图形序号的关系是解决本题的关键;

练习册系列答案
相关题目
如图,用黑白两色正形瓷砖铺设矩形地面,请观察下图并解答有关问题:
 |
⑴.在第n个图中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖,白色瓷砖共有 块;(用含n的代数式表示)
⑵.设铺设地面所用瓷砖的总块数为y,请写出y与⑴中的n的关系式: