题目内容
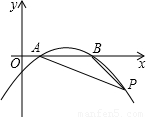
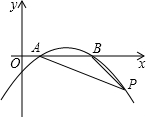
如下图,已知抛物线y= x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,
x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点, 它的横坐标为9,∠PBO=135°,cot∠PAB=
它的横坐标为9,∠PBO=135°,cot∠PAB= .
.
(1)求点P的坐标;(2)求抛物线的解析式.
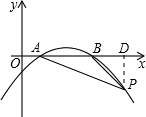 解:(1)过点P作PD⊥x轴,垂足为D.
解:(1)过点P作PD⊥x轴,垂足为D.∵∠PBO=135°,
∴∠PBD=45°,
∴PD=BD.
在Rt△PAD中,AD=AB+BD=4+PD,
∴cot∠PAD=
 ,
,解得:PD=3,
∴点P的坐标为(9,-3);
(2)∵OA=OD-AD=9-7=2,
∴点A的坐标为A(2,0),
将A、P两点坐标代入y=-
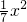 +bx+c中,得
+bx+c中,得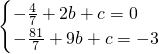 ,
,解得b=
 ,c=-
,c=-
∴抛物线的解析式y=-
 x2+
x2+ x-
x- .
.分析:(1)根据三角函数求点P的坐标,∠PBO=135°,即∠PBD=45°,有PD=BD,再根据余切cot∠PAB=
 求得.
求得.(2)求抛物线的解析式,先求出A,B的坐标,再运用代入法求出.
点评:此题主要考查了二次函数中结合三角函数求点的坐标,以及代入法求二次函数的解析式,此种题型是中考中热点问题,注意合理利用已知条件,切记忽略条件盲目分析.

练习册系列答案
相关题目
 它的横坐标为9,∠PBO=135°,cot∠PAB=
它的横坐标为9,∠PBO=135°,cot∠PAB=
 x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB=
x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB= .
.
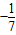 x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB=
x2+bx+c和x轴正半轴相交于A、B两点,AB=4,P为抛物线上的一点,它的横坐标为9,∠PBO=135°,cot∠PAB= .
.