题目内容
【背景】小明和小亮研究一道习题:“已知m>n>0,若分式
的分子、分母都加上1,所得的分式
的值增大了还是减小了?”.
小明想到了“用
减去
判断差的正负性”的思路;
小亮的想法是“可以直接将两个分式化成分母相同,再比较分子的大小”.
两人的解题思路都正确.
【问题】
(1)小亮提出问题:已知m>n>1,分式
的分子、分母都减去1后所得的分式
的值增大了还是减小了?请你探索解答这个问题.
(2)小明进一步提出问题:已知m>n>a,分式
的分子、分母都减去a后,所得分式
的值增大了还是减小了?请你探索解答这个问题.
| n |
| m |
| n+1 |
| m+1 |
小明想到了“用
| n |
| m |
| n+1 |
| m+1 |
小亮的想法是“可以直接将两个分式化成分母相同,再比较分子的大小”.
两人的解题思路都正确.
【问题】
(1)小亮提出问题:已知m>n>1,分式
| n |
| m |
| n-1 |
| m-1 |
(2)小明进一步提出问题:已知m>n>a,分式
| n |
| m |
| n-a |
| m-a |
分析:(1)先把
-
进行化简,再根据m>n>1进行判断即可;
(2)先把
-
进行化简,再分m>n>a>0,0>m>n>a,a<n<0<m,a<0<n<m四种情况进行讨论.
| n |
| m |
| n-1 |
| m-1 |
(2)先把
| n |
| m |
| n-a |
| m-a |
解答:解:(1)
-
=
=
,
∵m>n>1,
∴m-n>0,m(m-1)>0,
∴
>0,即
>
,
∴分式
的分子、分母都减去1后所得的分式
的值减小了;
(2)
-
=
=
,
∵m>n>a,
∴当m>n>a>0时,(m-n)a>0,m(m-a)>0,
∴
>
;
当0>m>n>a时,(m-n)a<0,m(m-a)<0,
∴
>0,
∴
>
;
当m>0,n<0时,a<n<0,
∴(m-n)a<0,m(m-a)>0,
∴
<0,即
<
;
当m>n>0,a<0时,(m-n)a<0,m(m-a)>0,
∴
<0,即
<
.
| n |
| m |
| n-1 |
| m-1 |
| n(m-1)-m(n-1) |
| m(m-1) |
| m-n |
| m(m-1) |
∵m>n>1,
∴m-n>0,m(m-1)>0,
∴
| m-n |
| m(m-1) |
| n |
| m |
| n-1 |
| m-1 |
∴分式
| n |
| m |
| n-1 |
| m-1 |
(2)
| n |
| m |
| n-a |
| m-a |
| n(m-a)-m(n-a) |
| m(m-a) |
| (m-n)a |
| m(m-a) |
∵m>n>a,
∴当m>n>a>0时,(m-n)a>0,m(m-a)>0,
∴
| n |
| m |
| n-a |
| m-a |
当0>m>n>a时,(m-n)a<0,m(m-a)<0,
∴
| (m-n)a |
| m(m-a) |
∴
| n |
| m |
| n-a |
| m-a |
当m>0,n<0时,a<n<0,
∴(m-n)a<0,m(m-a)>0,
∴
| (m-n)a |
| m(m-a) |
| n |
| m |
| n-a |
| m-a |
当m>n>0,a<0时,(m-n)a<0,m(m-a)>0,
∴
| (m-n)a |
| m(m-a) |
| n |
| m |
| n-a |
| m-a |
点评:本题考查的是分式的加减法,在解答(2)时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目


 如不能成功,请说明理由
如不能成功,请说明理由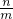 的分子、分母都加上1,所得的分式
的分子、分母都加上1,所得的分式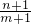 的值增大了还是减小了?”.
的值增大了还是减小了?”.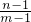 的值增大了还是减小了?请你探索解答这个问题.
的值增大了还是减小了?请你探索解答这个问题.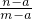 的值增大了还是减小了?请你探索解答这个问题.
的值增大了还是减小了?请你探索解答这个问题.