��Ŀ����
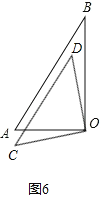
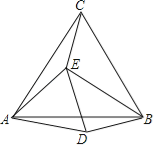
����Ŀ����һ�����ǰ��ֱ���غϷ��ã���ͼ1��ʾ��
��1��ͼ1����BEC�Ķ���Ϊ_________
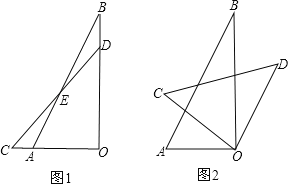
��2�����ǰ���AOB��λ�ñ��ֲ����������ǰ���COD����ֱ�Ƕ���O˳ʱ�뷽����ת��
�ٵ���ת��ͼ2��ʾλ��ʱ��ǡ��OD��AB�����ʱ��AOC�Ĵ�С��
���������ǰ���COD������O��ת��ֱ���ص�ͼ1λ�ã�����һ�����У��Ƿ�������COD����һ������ABƽ�У�������ڣ����㻭��ͼ�Σ���ֱ��д����Ӧ����AOC�Ĵ�С����������ڣ���˵�����ɣ�
���𰸡���1��165�㣨2����30���120�����
��������
�����������1������֪�������CAE=180�㩁60��=120�㣬�ٸ���������������������BEC�Ķ�����
��2������OD��AB�ɵ���BOD=��B=30�㣬������BOD+��BOC=90�����AOC+��BOC=90�������AOC��
�ڽ����ǰ���COD������O��ת��OC������ABƽ�У���ƽ�пɵ���COB=��B=30�㣬�Ӷ������AOC��
�⣺��1����CAE=180�㩁��BAO=180�㩁60��=120�㣬
���BEC=��C+��CAE=45��+120��=165�㣬
�ʴ�Ϊ��165�㣮
��2������OD��AB��
���BOD=��B=30�㣬
����BOD+��BOC=90�㣬��AOC+��BOC=90�㣬
���AOC=��BOD=30�㣮

�ڴ��ڣ���ͼ1����AOC=120�㣻
��ͼ2����AOC=165�㣻
��ͼ3����AOC=30�㣻
��ͼ4����AOC=150�㣻
��ͼ5����AOC=60�㣻
��ͼ6����AOC=15�㣮