题目内容
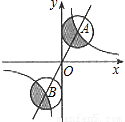
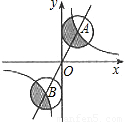
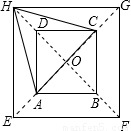
(2005•长春)图中有两个正方形,A、C两点在大正方形的对角线上,△HAC是等边三角形.若AB=2,求EF的长.(参考数据:sin30°= ,cos30°=
,cos30°=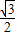 ,tan30°=
,tan30°=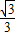 ;sin45°=
;sin45°=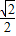 ,cos45°=
,cos45°=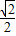 ,tan45°=1)
,tan45°=1)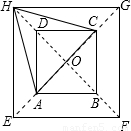
【答案】分析:根据题中所给的条件及等边三角形和正方形的性质,找到直角,直角三角形中解题,根据角的正弦值与三角形边的关系及勾股定理,然后再代入三角函数进行求解,求出EF边的长.
解答:解:在小正方形ABCD中,AB=2,则AC=2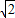 ,
,
在等边三角形ACH中,CH=2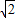 ,CO=
,CO=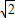 ,HO=
,HO=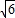 ,
,
在等腰直角三角形HOG中,HG=2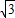 ,
,
即EF=2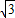 .
.
点评:本题利用了正方形的对角线是边的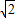 倍,等边三角形中三边相等,等腰直角三角形中斜边是直角边的
倍,等边三角形中三边相等,等腰直角三角形中斜边是直角边的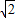 倍,主要考查边三角形和正方形的性质.
倍,主要考查边三角形和正方形的性质.
解答:解:在小正方形ABCD中,AB=2,则AC=2
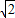 ,
,在等边三角形ACH中,CH=2
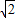 ,CO=
,CO=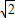 ,HO=
,HO=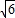 ,
,
在等腰直角三角形HOG中,HG=2
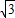 ,
,即EF=2
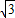 .
.点评:本题利用了正方形的对角线是边的
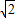 倍,等边三角形中三边相等,等腰直角三角形中斜边是直角边的
倍,等边三角形中三边相等,等腰直角三角形中斜边是直角边的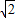 倍,主要考查边三角形和正方形的性质.
倍,主要考查边三角形和正方形的性质. 
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ,cos30°=
,cos30°=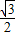 ,tan30°=
,tan30°=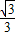 ;sin45°=
;sin45°=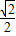 ,cos45°=
,cos45°=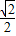 ,tan45°=1)
,tan45°=1)