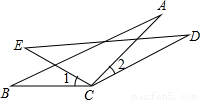
题目内容
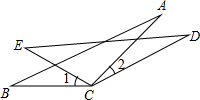已知CE=CB，∠1=∠2，AC=DC，
求证：AB=DE．
证明：∵∠1=∠2，∠BCE=∠1+∠ECA，∠DCE=∠2+∠ECA，
∴∠BCE=∠DCE．
在△ABC和△DCE中，
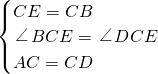
∴△ABC≌△DCE（SAS）．
∴AB=DE．
分析：欲证MB=MC，可利用判定两个三角形全等的方法“两边和它们的夹角对应相等的两个三角形全等”证△ABC≌△DCE，然后由全等三角形对应边相等得出．
点评：本题主要考查证明两个全等三角形全等的“边角边”的判定方法，本题比较简单．
∴∠BCE=∠DCE．
在△ABC和△DCE中，
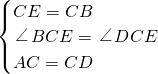
∴△ABC≌△DCE（SAS）．
∴AB=DE．
分析：欲证MB=MC，可利用判定两个三角形全等的方法“两边和它们的夹角对应相等的两个三角形全等”证△ABC≌△DCE，然后由全等三角形对应边相等得出．
点评：本题主要考查证明两个全等三角形全等的“边角边”的判定方法，本题比较简单．
练习册系列答案
相关题目
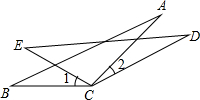已知CE=CB，∠1=∠2，AC=DC，
