题目内容
已知,纸片⊙O的半径为2 ,如图1. 沿着弦AB 折叠操作。
(1)如图2 ,当折叠后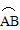 的经过圆心O时,求
的经过圆心O时,求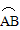 的长度;
的长度;
(2)如图3,当弦AB=2时,求折叠后⊙O所在圆的圆心O′到弦AB的距离;
(3)在如图1中,将纸片⊙O沿着弦CD折叠操作:
①如图4,当AB∥CE时,折叠后的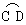 和
和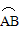 所在圆外切与点P时,设点O到弦CD,AB的距离之和为d,试求d的值;
所在圆外切与点P时,设点O到弦CD,AB的距离之和为d,试求d的值;
②如图5,当AB与CD不平行时,折叠后的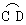 和
和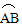 所在圆外切与点P,点M,N分别为AB,CD的中点试探究四边形OMPN的形状,并证明。
所在圆外切与点P,点M,N分别为AB,CD的中点试探究四边形OMPN的形状,并证明。
(1)如图2 ,当折叠后
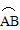 的经过圆心O时,求
的经过圆心O时,求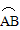 的长度;
的长度; (2)如图3,当弦AB=2时,求折叠后⊙O所在圆的圆心O′到弦AB的距离;
(3)在如图1中,将纸片⊙O沿着弦CD折叠操作:
①如图4,当AB∥CE时,折叠后的
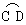 和
和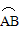 所在圆外切与点P时,设点O到弦CD,AB的距离之和为d,试求d的值;
所在圆外切与点P时,设点O到弦CD,AB的距离之和为d,试求d的值; ②如图5,当AB与CD不平行时,折叠后的
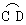 和
和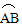 所在圆外切与点P,点M,N分别为AB,CD的中点试探究四边形OMPN的形状,并证明。
所在圆外切与点P,点M,N分别为AB,CD的中点试探究四边形OMPN的形状,并证明。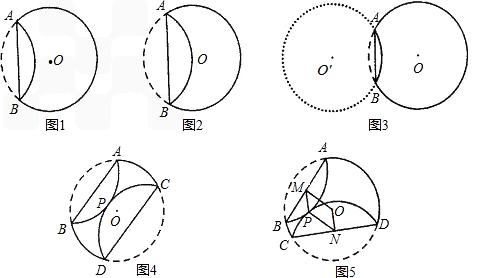
| 解:(1)可以过点O作OE垂直于弦AB,并连接AE,BE,BO,AO, 由图形的对称性可知四边形AEOB 为菱形,△AEO,△BEO均为等边三角形,∠AOB=120°, 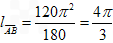 ; ;(2).折叠后的圆O′与圆O是等圆,设折叠后  所在圆的圆心O,可过O′作AB的垂线段即为m, 所在圆的圆心O,可过O′作AB的垂线段即为m, m=tan60°×1= 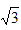 ; ;(3)可作AB垂线,交圆与点E,点G,且经过点P,EF必定垂直且平分AB,CD。GE=GP,HP=HF; 距离之和为d= (GE+GP+HP+HF)÷2=4÷2=2; (4)可设点K,点L分别是  , ,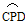 所在圆的圆心,连接KL, 所在圆的圆心,连接KL,∵折叠后⊙K,⊙O,⊙L均是等圆 ∵点K与点O, 点L与点O是分别关于AB,CD的对称点, ∴点M,点N分别是OK,OL的中点; 连心线KL必定经过外切点P;点M,N,P分别是△KOL三边的中点, ∴MP=NO=  OL, OL,MP∥OL, ∴四边形OMPN 为平行四边形。 |
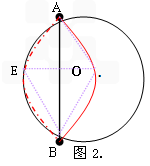 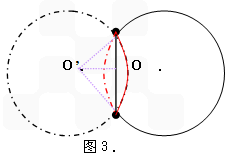 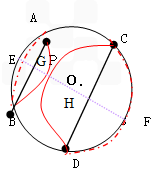 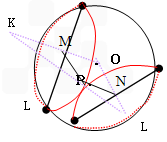 图5 图4 |

练习册系列答案
相关题目