题目内容
如图1,将△ABC的三个顶点的横坐标同时乘以-1得到三个新的顶点A′,B′,C′,则△ABC与△A′B′C′关于y轴对称(对称变换);如图2,将⊙O(x2+y2=2)向上平移2个单位,在向右平移3个单位得到⊙A (x-3)2+(y-2)2=2(平移变换);如图3,把y=x2的图象上点的横坐标不变,所有点的纵坐标同时乘以4得到一个新图象,则新图象的解析式为| 1 |
| 4 |
(1)y=x2-x+1的图象关于原点对称图象的解析式为
(2)将y=-
| 1 |
| x |
(3)将y=5x+1的图象所有点的纵坐标不变,横坐标缩短为原来的
| 1 |
| 5 |
(4)试探究:抛物线y=3x2-6x+1是由抛物线y=x2通过怎样的变换而得到的?
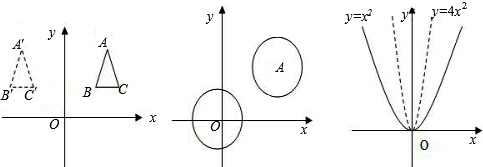
分析:(1)关于原点对称,那么所求图象的开口向下,二次项的系数与原二次项的系数互为相反数,对称轴在y轴的左侧,那么b<0,与y轴的交点在y轴的下方,为原来交点的相反数;
(2)根据平移规律,在横坐标处加3,纵坐标处减4即可;
(3)根据伸缩规律,让横坐标乘5即可得到相应函数解析式;
(4)把抛物线y=3x2-6x+1整理为顶点式,并且两边都除以二次项系数,看顶点是如何变化的及y是如何变化的即可.
(2)根据平移规律,在横坐标处加3,纵坐标处减4即可;
(3)根据伸缩规律,让横坐标乘5即可得到相应函数解析式;
(4)把抛物线y=3x2-6x+1整理为顶点式,并且两边都除以二次项系数,看顶点是如何变化的及y是如何变化的即可.
解答:解:(1)关于原点对称,那么所求图象的开口向下,开口大小不变,
∴a=-1,
∵变换后对称轴在y轴左侧,
∴b=-1,
∵变换后与y轴交于负半轴,
∴c=-1,
∴y=-x2-x-1;
(2)y=-
-4;
(3)∵横坐标缩短为原来的
,
∴解析式为:y=25x+1;
(4)y=3x2-6x+1=3(x-1)2-2,
∴
=(x-1)2-
,
∴y=x2向右平移1个单位,再向下平移
个单位,得:y=(x-1)2-
,
那么横坐标不变,纵坐标伸长为原来的3倍可得抛物线y=3x2-6x+1.
∴a=-1,
∵变换后对称轴在y轴左侧,
∴b=-1,
∵变换后与y轴交于负半轴,
∴c=-1,
∴y=-x2-x-1;
(2)y=-
| 1 |
| x+3 |
(3)∵横坐标缩短为原来的
| 1 |
| 5 |
∴解析式为:y=25x+1;
(4)y=3x2-6x+1=3(x-1)2-2,
∴
| y |
| 3 |
| 2 |
| 3 |
∴y=x2向右平移1个单位,再向下平移
| 2 |
| 3 |
| 2 |
| 3 |
那么横坐标不变,纵坐标伸长为原来的3倍可得抛物线y=3x2-6x+1.
点评:解决本题的关键是理解平移变化中左右平移只改变横坐标的值,左加右减;上下平移只改变常数,上加下减;伸缩变化中,坐标是原来坐标的n倍,那么所求的解析式的坐标应为原来坐标的
倍.
| 1 |
| n |

练习册系列答案
相关题目
 18、如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,则A点的对应点D的坐标是( )
18、如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,则A点的对应点D的坐标是( )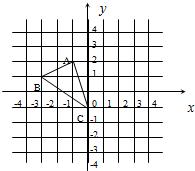 21、如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,则A点的对应点D的坐标是
21、如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,则A点的对应点D的坐标是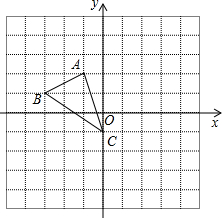 如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,
如图,若将△ABC的绕点C顺时针旋转90°后得到△DEC,