题目内容
先作半径为1的圆,再作它的内接正三角形,接着作上述内接正三角形的内切圆,再作上述内切圆的内接正三角形,…,则按以上规律作出的第2008个圆的半径为
- A.
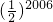
- B.
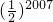
- C.
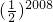
- D.
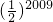
B
分析:任何两个圆都一定相似,根据等边三角形的外接圆与内切圆的关系,即可求得相似比,从而求解.
解答: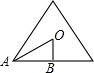 解:O是内心,连接OA,OB是内切圆的半径,则OA=1,∠OAB=30°.
解:O是内心,连接OA,OB是内切圆的半径,则OA=1,∠OAB=30°.
∴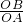 =
=
则内切圆与外接圆的相似比是: .
.
∴第一个圆的半径是1,后面的圆都与前边相邻的圆相似,相似比是: .
.
故第二个圆的半径是( ),第三个是:(
),第三个是:( )2,第四个是:(
)2,第四个是:( )3…
)3…
∴第2008个圆的半径为( )2007.
)2007.
故选B.
点评:本题主要考查了正多边形的计算,求得相似比,得到相邻两圆的关系是解题关键.
分析:任何两个圆都一定相似,根据等边三角形的外接圆与内切圆的关系,即可求得相似比,从而求解.
解答:
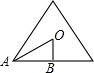 解:O是内心,连接OA,OB是内切圆的半径,则OA=1,∠OAB=30°.
解:O是内心,连接OA,OB是内切圆的半径,则OA=1,∠OAB=30°.∴
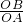 =
=
则内切圆与外接圆的相似比是:
 .
.∴第一个圆的半径是1,后面的圆都与前边相邻的圆相似,相似比是:
 .
.故第二个圆的半径是(
 ),第三个是:(
),第三个是:( )2,第四个是:(
)2,第四个是:( )3…
)3…∴第2008个圆的半径为(
 )2007.
)2007.故选B.
点评:本题主要考查了正多边形的计算,求得相似比,得到相邻两圆的关系是解题关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
先作半径为
的圆的内接正方形,接着作上述内接正方形的内切圆,再作上述内切圆的内接正方形,…,则按以上规律作出的第7个圆的内接正方形的边长为( )
| ||
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
先作半径为1的圆,再作它的内接正三角形,接着作上述内接正三角形的内切圆,再作上述内切圆的内接正三角形,…,则按以上规律作出的第2008个圆的半径为( )
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|