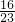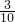题目内容
一个分数的分母比分子大7,如果把分子加上17,分母减去4,那么所得的分数等于原来分数的倒数,原分数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:关系式为:原来的分数×后来所得的分数=1,把相关数值代入可得分数的分子,也就求得了原来的分数.
解答:解:设原来分数的分子为x,则分母为(x+7),
分子加上17,分母减去4,所得的分式为:
,
根据互为倒数的两数之积为1可得,
×
=1,
解得x=3,
∴原分数为
.
故选D.
分子加上17,分母减去4,所得的分式为:
| x+17 |
| x+3 |
根据互为倒数的两数之积为1可得,
| x |
| x+7 |
| x+17 |
| x+3 |
解得x=3,
∴原分数为
| 3 |
| 10 |
故选D.
点评:考查分式方程的应用;得到两个分数的关系式是解决本题的关键.

练习册系列答案
相关题目