题目内容
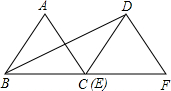 如图,△ABC是面积为
如图,△ABC是面积为 的等边三角形,将△ABC沿直线BC平移到△DEF,使点E与点C重合,连接BD,则BD的长是
的等边三角形,将△ABC沿直线BC平移到△DEF,使点E与点C重合,连接BD,则BD的长是
- A.2

- B.

- C.2
- D.2

A
分析:利用平移的性质得出BC,CF的长,再利用勾股定理以及等腰三角形的性质得出BD长.
解答:∵△ABC是面积为 的等边三角形,
的等边三角形,
∴等边三角形的边长为2,
∴BC=CF=2,
∵BC=DC,∠DCF=60°,
∴∠CBD=∠CDB=30°,∠BDF=90°,
∴BD= =2
=2 .
.
故选:A.
点评:此题主要考查了平移的性质以及等边三角形的性质,根据题意得出∠BDF=90°是解决问题的关键.
分析:利用平移的性质得出BC,CF的长,再利用勾股定理以及等腰三角形的性质得出BD长.
解答:∵△ABC是面积为
 的等边三角形,
的等边三角形,∴等边三角形的边长为2,
∴BC=CF=2,
∵BC=DC,∠DCF=60°,
∴∠CBD=∠CDB=30°,∠BDF=90°,
∴BD=
 =2
=2 .
.故选:A.
点评:此题主要考查了平移的性质以及等边三角形的性质,根据题意得出∠BDF=90°是解决问题的关键.

练习册系列答案
相关题目
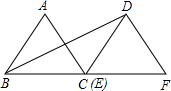 如图,△ABC是面积为
如图,△ABC是面积为| 3 |
A、2
| ||
B、
| ||
| C、2 | ||
D、2
|
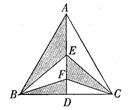
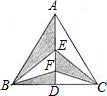 如图,△ABC是面积为a的等边三角形,AD是BC边上的高,点E、F是AD上的两点.则图中阴影部分的面积为
如图,△ABC是面积为a的等边三角形,AD是BC边上的高,点E、F是AD上的两点.则图中阴影部分的面积为 如图,△ABC是面积为18cm的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )
如图,△ABC是面积为18cm的等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积为( )