题目内容
一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为| 1 | 3 |
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
分析:(1)根据摸得黑球的概率为
,假设出白球个数直接得出答案;
(2)利用先随机从口袋中摸出一球,不放回,得出树状图即可.
| 1 |
| 3 |
(2)利用先随机从口袋中摸出一球,不放回,得出树状图即可.
解答: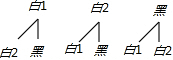 解:(1)∵一个口袋中有1个黑球和若干个白球,从中任意摸取一个球,摸得黑球的概率为
解:(1)∵一个口袋中有1个黑球和若干个白球,从中任意摸取一个球,摸得黑球的概率为
.
∴假设白球有x个,
∴
=
,
∴x=2.
∴口袋中白球的个数为2个;
(2)∵先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.
∴两次都摸到白球的概率为:
.
 解:(1)∵一个口袋中有1个黑球和若干个白球,从中任意摸取一个球,摸得黑球的概率为
解:(1)∵一个口袋中有1个黑球和若干个白球,从中任意摸取一个球,摸得黑球的概率为| 1 |
| 3 |
∴假设白球有x个,
∴
| 1 |
| 1+x |
| 1 |
| 3 |
∴x=2.
∴口袋中白球的个数为2个;
(2)∵先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.
∴两次都摸到白球的概率为:
| 1 |
| 3 |
点评:此题主要考查了树状图法求概率,根据已知得出树状图注意按要求从口袋中摸出一球,不放回,容易在这个地方犯错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目