题目内容
已知：如图，小正六边形的边长是1，大正六边形的边长的2，A是小正六边形的一个顶点，若小正六边形沿大正六边形内侧滚动一周，回到原来的位置，则点A的行程为
分析：首先画出点A运动的大致路线，确定不同运动过程中，A点所走过的弧所在圆的圆心和半径，然后根据弧长公式求出它们的值，再相加即可．
解答：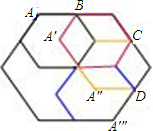
解：如右图；
当点A运动到A′时，A点运动的距离为以B为圆心，AB为半径，∠ABA′为圆心角的弧长；
即C1=
=
；
当点A′运动到A″时，A点运动的距离为以C为圆心，CA′为半径，∠A′CA″为圆心角的弧长；
易求得CA′=2，∠A′CA″=60°，
则C2=
=
；
当点A″运动到A'''时，A点运动的距离为以D为圆心，DA'''为半径，∠A″DA'''为圆心角的弧长，
同上可求得C3=C1=
；
故从A到A'''，一共运动的距离为：C1+C2+C3=
；
当从点A'''到A时，A点运动的规律同上，故A点转动一周的距离为：
．
解：如右图；当点A运动到A′时，A点运动的距离为以B为圆心，AB为半径，∠ABA′为圆心角的弧长；
即C1=
| 60×π×1 |
| 180 |
| π |
| 3 |
当点A′运动到A″时，A点运动的距离为以C为圆心，CA′为半径，∠A′CA″为圆心角的弧长；
易求得CA′=2，∠A′CA″=60°，
则C2=
| 60×π×2 |
| 180 |
| 2π |
| 3 |
当点A″运动到A'''时，A点运动的距离为以D为圆心，DA'''为半径，∠A″DA'''为圆心角的弧长，
同上可求得C3=C1=
| π |
| 3 |
故从A到A'''，一共运动的距离为：C1+C2+C3=
| 4π |
| 3 |
当从点A'''到A时，A点运动的规律同上，故A点转动一周的距离为：
| 8π |
| 3 |
点评：此题主要考查了正多边形的性质以及弧长的计算公式，找出A点不同运动过程的圆心和半径是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
