题目内容
已知反比例函数y=
的图象和一次函数y=kx-7的图象都经过点P(m,2).
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a和a+2,求a的值.
| 12 |
| x |
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a和a+2,求a的值.

(1)∵点P(m,2)在函数y=
的图象上,
∴m=6,
∵一次函数y=kx-7的图象经过点P(6,2),
得6k-7=2,
∴k=
,
∴所求的一次函数解析式是y=
x-7;
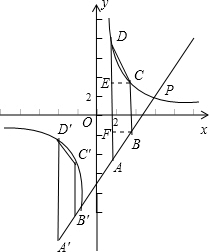
(2)过B作BF⊥AD,过C作CE⊥AD,
∵点A、B的横坐标分别是a和a+2,
∴可得,A(a,
-7),B(a+2,
-4),
C(a+2,
),D(a,
),
∵AB=CD,
∴在Rt△CDE与Rt△ABF中,
由勾股定理得:CD2=DE2+EC2=22+(
-
)2,
AB2=AF2+BF2=22+32,
∵等腰梯形ABCD,
∴AB=CD,即22+32=22+(
-
)2,
即
-
=±3,
①由
-
=3,化简得a2+2a+8=0,方程无实数根,
②由
-
=-3,化简得a2+2a-8=0,
∴a1=-4,a2=2.
经检验,a1=-4,a2=2均为所求的值.
| 12 |
| x |
∴m=6,
∵一次函数y=kx-7的图象经过点P(6,2),
得6k-7=2,
∴k=
| 3 |
| 2 |
∴所求的一次函数解析式是y=
| 3 |
| 2 |

(2)过B作BF⊥AD,过C作CE⊥AD,
∵点A、B的横坐标分别是a和a+2,
∴可得,A(a,
| 3a |
| 2 |
| 3a |
| 2 |
C(a+2,
| 12 |
| a+2 |
| 12 |
| a |
∵AB=CD,
∴在Rt△CDE与Rt△ABF中,
由勾股定理得:CD2=DE2+EC2=22+(
| 12 |
| a+2 |
| 12 |
| a |
AB2=AF2+BF2=22+32,
∵等腰梯形ABCD,
∴AB=CD,即22+32=22+(
| 12 |
| a+2 |
| 12 |
| a |
即
| 12 |
| a+2 |
| 12 |
| a |
①由
| 12 |
| a+2 |
| 12 |
| a |
②由
| 12 |
| a+2 |
| 12 |
| a |
∴a1=-4,a2=2.
经检验,a1=-4,a2=2均为所求的值.

练习册系列答案
相关题目



 取值范围.
取值范围.