题目内容
现场学习:我们知道,若锐角α的三角函数值为sinα=m,则可通过计算器得到角α的大小,这时我们用arcsinm来表示α,
记作:α=arcsinm;若cosα=m,则记α=arccosm;若tanα=m,则记α=arctanm.
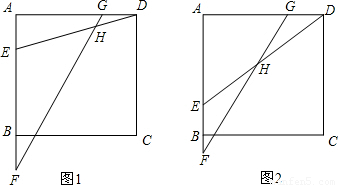
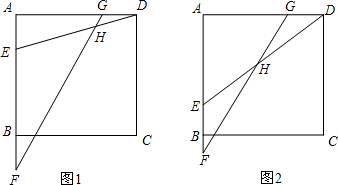
解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连接ED,FG,交点为H.
(1)如图1,若AE=BF=GD,请直接写出∠EHF=________°;
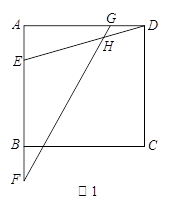
(2)如图2,若EF= CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时,∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时,∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.

 解:(1)45°;
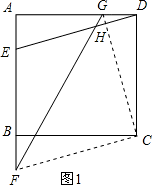
解:(1)45°;连接FC和CG(如图1),由题意可知ABCD为正方形,AE=BF=GD,
∴△AED≌△BFC≌△DGC(SAS),
∴CF=GC,∠AED=∠BFC,∠BCF=∠DCG,
∴ED∥FC,
∴∠EHF=∠GFC,
又∵∠BCD=90°=∠BCG+∠GCD=∠BCG+∠BCF=∠GCF,
∴△GCF是等腰直角三角形,
∴∠GFC=∠FGC=45°,
∴∠EHF=45°;
(2)答:不会变化.
证明
 :如图2,过点F作FM∥ED交CD于M,连接GM.
:如图2,过点F作FM∥ED交CD于M,连接GM.∵正方形ABCD中,AB∥CD,
∴四边形EFMD为平行四边形.
∴EF=DM,DE=FM.
∴∠3=∠4,∠EHF=∠HFM=α.
∵EF=
 CD,GD=
CD,GD= AE,
AE,∴
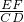 =
= =
= .
.∴
 ,
,∵∠A=∠GDM=90°,
∴△DGM∽△AED.
∴
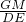 =
= ,∠1=∠2,
,∠1=∠2,∴
 =
= ,
,
∵∠2+∠3=90°,∠1=∠2,∠3=∠4.
∴∠1+∠4=90°.
∴∠GMF=90°.
在Rt△GFM中,tanα=
 =
= .
.∴α=arctan
 .
.另解2:作EM⊥CD于M,连接GM,FM可解,应该简单些.
分析:(1)作辅助线,连接FC和GC,可证得△FCG为等腰直角三角形,利用∠EHF=∠GFC=45°,问题可求.
(2)作辅助线,过点F作FM∥ED交CD于M,连接GM,则会有∠EHF=∠GFM,将问题转化到△GFM中,据已知正方形关系,可证得四边形EFMD为平行四边形,△GFM为直角三角形,于是,α可求.
点评:本题综合性强,难度较大,考查学生对辅助线的运用和综合推理能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 (2)如图2,若EF =
(2)如图2,若EF =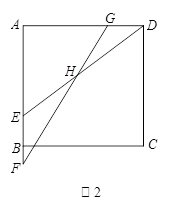
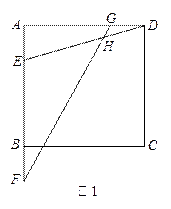 (2)如图2,若EF=
(2)如图2,若EF=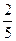 CD,GD=
CD,GD=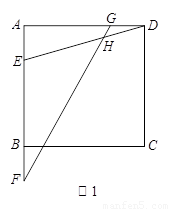 (2)如图2,若EF =
(2)如图2,若EF =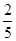 CD,GD=
CD,GD=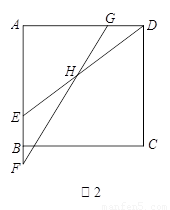
 CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时,∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时,∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.