Question

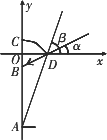
如图,AB是高为1.46米的窗户(窗户朝南),该窗户的遮阳篷呈抛物线形，在图中坐标系内的表达式为y=-x²+0.25，已知该地一年中冬至日正午时刻太阳光线与地面的夹角最小为α，夏至日正午时刻太阳光线与地面的夹角最大为β，且β="73°30′." 若该遮阳篷使冬至日正午时刻太阳光线刚好全部射入室内，夏至日正午时刻太阳光刚好全部不射入室内.求α的度数及遮阳篷顶部到窗户上沿的距离.

 

Answer 1

【答案】

0.48米

【解析】

试题分析：先求得抛物线与x轴的交点即点D的坐标，再在Rt△AOD中，根据∠ADO的正切函数求得AO的长，再根据AB的长求得OB的长，在Rt△BOD中，求得∠BDO的正切值，即可得到α=24°42′的度数，从而得到OC的长，即可求得结果.

由y=0得-x²+0.25=0

解得得x=0.5(舍负)

故OD=0.5(米).

在Rt△AOD中，AO=OD·tan∠ADO=0.5tanβ=0.5×tan73°30′≈1.69.

又AB=1.46

故OB≈0.23米.

在Rt△BOD中，tan∠BDO=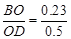=0.46

故∠BDO≈24°42′，即α=24°42′.

令x=0，得y=0.25，

故OC=0.25

从而BC=0.25+0.23=0.48米.

考点：解直角三角形的应用

点评：直角三角形的判定和性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.