题目内容
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连接CF. 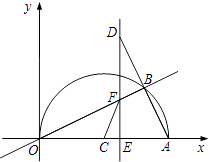
(1)当∠AOB=30°时,求弧AB的长度;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似?若存在,请求出此时点E的坐标;若不存在,请说明理由.
【答案】
(1)解:连接BC,
∵A(10,0),∴OA=10,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
∴弧AB的长= ![]()
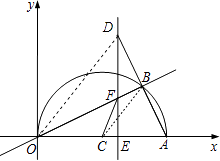
(2)解:①若D在第一象限,
连接OD,
∵OA是⊙C直径,
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE= ![]() =
= ![]() ,
,
∴AE=AO﹣OE=10﹣6=4,
由∠AOB=∠ADE=90°﹣∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴ ![]() ,即
,即 ![]() ,
,
∴EF=3;
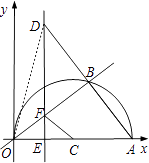
②若D在第二象限,
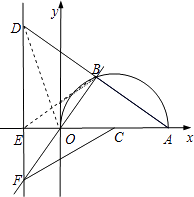
连接OD,
∵OA是⊙C直径,
∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE= ![]() =
= ![]() ,
,
∴AE=AO+OE=10+6=16,
由∠AOB=∠ADE=90°﹣∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EF=12;
∴EF=3或12;
(3)解:设OE=x,
①当交点E在O,C之间时,由以点E、C、F为顶点的三角
形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,
当∠ECF=∠BOA时,此时△OCF为等腰三角形,点E为OC
中点,即OE= ![]() ,
,
∴E1( ![]() ,0);
,0);
当∠ECF=∠OAB时,有CE=5﹣x,AE=10﹣x,
∴CF∥AB,有CF= ![]() ,
,
∵△ECF∽△EAD,
∴ ![]() ,即
,即 ![]() ,解得:
,解得: ![]() ,
,
∴E2( ![]() ,0);
,0);
②当交点E在点C的右侧时,
∵∠ECF>∠BOA,
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连接BE,
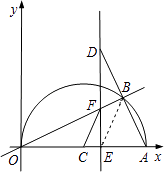
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE,
∴ ![]() ,
,
∵∠ECF=∠BAO,∠FEC=∠DEA=90°,
∴△CEF∽△AED,
∴ ![]() ,
,
而AD=2BE,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() <0(舍去),
<0(舍去),
∴E3( ![]() ,0);
,0);
③当交点E在点O的左侧时,
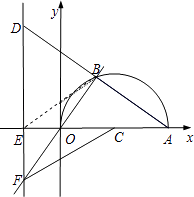
∵∠BOA=∠EOF>∠ECF.
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO
连接BE,得BE= ![]() =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴ ![]() ,
,
又∵∠ECF=∠BAO,∠FEC=∠DEA=90°,
∴△CEF∽△AED,
∴ ![]() ,
,
而AD=2BE,
∴ ![]() ,
,
∴ ![]() ,
,
解得x1= ![]() ,x2=
,x2= ![]() (舍去),
(舍去),
∵点E在x轴负半轴上,
∴E4( ![]() ,0),
,0),
综上所述:存在以点E、C、F为顶点的三角形与△AOB相似,
此时点E坐标为:E1( ![]() ,0)、E2(
,0)、E2( ![]() ,0)、E3(
,0)、E3( ![]() ,0)、E4(
,0)、E4( ![]() ,0).
,0).
【解析】(1)连接BC,由已知得∠ACB=2∠AOB=60°,AC= ![]() AO=5,根据弧长公式求解;(2)连接OD,由垂直平分线的性质得OD=OA=10,又DE=8,在Rt△ODE中,由勾股定理求OE,依题意证明△OEF∽△DEA,利用相似比求EF;(3)存在.当以点E、C、F为顶点的三角形与△AOB相似时,分为①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,②当交点E在点C的右侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,③当交点E在点O的左侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,三种情况,分别求E点坐标.
AO=5,根据弧长公式求解;(2)连接OD,由垂直平分线的性质得OD=OA=10,又DE=8,在Rt△ODE中,由勾股定理求OE,依题意证明△OEF∽△DEA,利用相似比求EF;(3)存在.当以点E、C、F为顶点的三角形与△AOB相似时,分为①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,②当交点E在点C的右侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,③当交点E在点O的左侧时,要使△ECF与△BAO相似,只能使∠ECF=∠BAO,三种情况,分别求E点坐标.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】某汽车行驶时油箱中余油量Q(L)与行驶时间t(h)的关系如表:
行驶时间t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
(1)汽车行驶之前油箱中有汽油多少升?
(2)用行驶时间t的代数式表示余油量Q(直接写出答案);
(3)当t=![]() 时,求余油量Q的值.
时,求余油量Q的值.