题目内容
(2008•张家界)已知直线y=-x-1与x、y轴分别交于A、B曰两点,将其向右平移4个单位所得直线分别与x、y轴交于C、D两点.(1)求C、D两点的坐标;
(2)求过A、C、D三点的抛物线的解析式;
(3)在(2)中所求抛物线的对称轴上,是否存在点P,使△PAB为等腰三角形?若存在,求出所有的点P的坐标;若不存在,请说明理由.
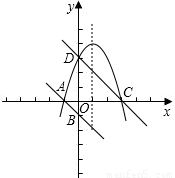
【答案】分析:(1)求出直线CD的解析式,再求出直线与坐标轴的交点坐标.
(2)已知A、C、D三点的坐标,根据待定系数法就可以求出抛物线的解析式.
(3)应分AB为腰和AB为底两种情况进行讨论.
解答:解:(1)把直线y=-x-1向右平移四个单位长度所得的直线的解析式是:y=-(x-4)-1,
即y=-x+3,在各个函数中分别令x=0,y=0,
解得y=3和x=3,
因而交点坐标是:C(3,0)D(0,3)
(2)设解析式为y=ax2+bx+c
把A(-l,0)D(0,3)C(3,0)代入得:
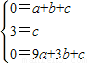
解得:
∴过A、C、D三点的抛物线的解析式为y=-x2+2x+3;
(3)存在.∵y=x2+2x+3的对称轴为直线x=- ,即x=1
,即x=1
当AB为腰时,易知点P坐标为(1,0)
当AB为底时,点P在AB垂直平分线y=x和x=1的交点处,此时点P的坐标为(1,1)
综上所述这样的点P有(1,0)和(1,1)两个.
点评:本题主要考查了函数平移是解析式的变化关系,以及待定系数法求函数的解析式.
(2)已知A、C、D三点的坐标,根据待定系数法就可以求出抛物线的解析式.
(3)应分AB为腰和AB为底两种情况进行讨论.
解答:解:(1)把直线y=-x-1向右平移四个单位长度所得的直线的解析式是:y=-(x-4)-1,
即y=-x+3,在各个函数中分别令x=0,y=0,
解得y=3和x=3,
因而交点坐标是:C(3,0)D(0,3)
(2)设解析式为y=ax2+bx+c
把A(-l,0)D(0,3)C(3,0)代入得:
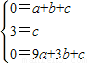
解得:

∴过A、C、D三点的抛物线的解析式为y=-x2+2x+3;
(3)存在.∵y=x2+2x+3的对称轴为直线x=-
 ,即x=1
,即x=1当AB为腰时,易知点P坐标为(1,0)
当AB为底时,点P在AB垂直平分线y=x和x=1的交点处,此时点P的坐标为(1,1)
综上所述这样的点P有(1,0)和(1,1)两个.
点评:本题主要考查了函数平移是解析式的变化关系,以及待定系数法求函数的解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目