题目内容
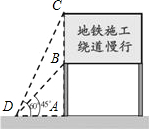为了缓解长沙市区内一些主要路段交通拥挤的现状，交警队在一些主要路口设立了交通路况显示牌（如图）．已知立杆AB高度是3m，从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°．求路况显示牌BC的高度．
解：∵在Rt△ADB中，∠BDA=45°，AB=3，
∴DA=3．
在Rt△ADC中，∠CDA=60°，
∴tan60°=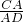
，
∴CA=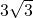
．
∴BC=CA-BA=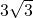（-3）米．
答：路况显示牌BC的高度是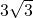（-3）米．
分析：在Rt△ABD中，知道了已知角的对边，可用正切函数求出邻边AD的长；同理在Rt△ABC中，知道了已知角的邻边，用正切值即可求出对边AC的长；进而由BC=AC-AB得解．
点评：当两个直角三角形有公共边时，先求出这条公共边的长是解答此类题的一般思路．
∴DA=3．
在Rt△ADC中，∠CDA=60°，
∴tan60°=
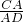，∴CA=
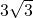． ∴BC=CA-BA=（
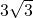-3）米．答：路况显示牌BC的高度是（
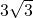-3）米． 分析：在Rt△ABD中，知道了已知角的对边，可用正切函数求出邻边AD的长；同理在Rt△ABC中，知道了已知角的邻边，用正切值即可求出对边AC的长；进而由BC=AC-AB得解．
点评：当两个直角三角形有公共边时，先求出这条公共边的长是解答此类题的一般思路．
练习册系列答案
相关题目
在方格纸上，每个小格的顶点叫做格点，以格点为顶点的三角形叫做格点三角形．如图在4×4的方格纸上以AB为边的格点△ABC的面积为2个平方单位，完成下列问题：
如图，梯形ABCD中，AD∥BC，中位线EF分别与BD、AC交于点G、H．若AD=6，BC=10，则GH=________．
）2，则a与b的关系是________．