Question

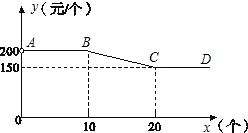永定土楼是世界文化遗产“福建土楼”的组成部分，是闽西的旅游胜地．“永定土楼”模型深受游客喜爱．图中折线（AB∥CD∥x轴）反映了某种规格土楼模型的单价y（元）与购买数量x（个）之间的函数关系．
（1）求当10≤x≤20时，y与x的函数关系式；
（2）已知某旅游团购买该种规格的土楼模型总金额为2625元，问该旅游团共购买这种土楼模型多少个？（总金额=数量×单价）

Answer 1

分析：（1）由图象可知，该直线过点（10，200），（20，150），利用待定系数法即可求出其解析式；
（2）因为购买该种规格的土楼模型，总金额为2625元，若单价为200元则个数应不大于10，总价应不超过2000元；
若单价为150元，则其个数应不少于20，总价应不小于3000元．
所以此次购买个数应不小于10且不大于20．
y与x之间应满足（1）中所求的关系，利用xy=2625．即可求出答案．

解答：解：（1）当10≤x≤20时，设y=kx+b（k≠0）（11分）
依题意，得

10k+b=200 20k+b=150

（3分）
解得

k=-5 b=250

（5分）
∴当10≤x≤20时，y=-5x+250；（6分）

（2）∵10×200＜2625＜20×150
∴10＜x＜20（8分）
依题意，得xy=x（-5x+250）=2625（10分）
即x²-50x+525=0
解得x₁=15，x₂=35（舍去）
∴只取x=15．（12分）
答：该旅游团共购买这种土楼模型15个．（13分）

点评：本题需仔细分析函数图象，利用待定系数法解决问题．