题目内容
 24、如图,已知BD是∠ABC的角平分线,E的BD上一点,EF∥BC,交AB于点F,FG∥EC交BC于G,你能说明BF与CG相等吗?说明理由.
24、如图,已知BD是∠ABC的角平分线,E的BD上一点,EF∥BC,交AB于点F,FG∥EC交BC于G,你能说明BF与CG相等吗?说明理由.分析:由于EF∥BC,FG∥EC易知四边形FGCE是平行四边形,故CG=EF;若证BF=CG,需证得BF=EF;△BFE中,由于EF∥BC,即∠FEB=∠CBE,而∠EBF=∠EBC,故∠FEB=∠FBE,即△BFE是等腰三角形,由此得证.
解答:解:BF与CG相等;理由如下:
∵BD平分∠ABC,
∴∠ABD=∠CBD;
∵EF∥BC,
∴∠FEB=∠CBD;
∴∠FBD=∠FEB,即BF=EF;
∵EF∥GC,FG∥EC,
∴四边形EFGC是平行四边形;
∴EF=CG;
∴BF=CG.
∵BD平分∠ABC,
∴∠ABD=∠CBD;
∵EF∥BC,
∴∠FEB=∠CBD;
∴∠FBD=∠FEB,即BF=EF;
∵EF∥GC,FG∥EC,
∴四边形EFGC是平行四边形;
∴EF=CG;
∴BF=CG.
点评:本题考查了平行四边形及等腰三角形的判定和性质.熟练掌握性质定理和判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
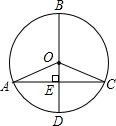 如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )| A、30° | B、40° | C、50° | D、60° |
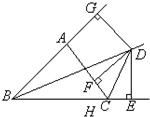 14、如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是
14、如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是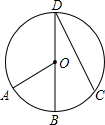 (2012•苏州)如图,已知BD是⊙O的直径,点A、C在⊙O上,
(2012•苏州)如图,已知BD是⊙O的直径,点A、C在⊙O上,
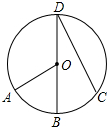 如图,已知BD是⊙O的直径,点A、C在⊙O上,
如图,已知BD是⊙O的直径,点A、C在⊙O上,