题目内容
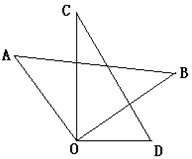
 24、将一副三角板的直角顶点重合放置,如图所示:
24、将一副三角板的直角顶点重合放置,如图所示:(1)写出图中以O为顶点的相等的角;
(2)若∠AOD=125°,求∠BOC的度数;
(3)判断∠AOD与∠BOC之间具有何种数量关系当三角板AOB绕O点旋转时,这种关系是否有变化?请说明理由.
分析:(1)图中有两个直角,再根据同角的余角相等即可找出;
(2)若∠AOD=125°,则∠AOC或∠BOD即可求出,然后根据余角的性质即可求出∠BOC;
(3)根据三角形内角和外角的关系解答.
(2)若∠AOD=125°,则∠AOC或∠BOD即可求出,然后根据余角的性质即可求出∠BOC;
(3)根据三角形内角和外角的关系解答.
解答:解:(1)∵∠AOB与∠COD为直角∴∠AOB=∠COD
∵∠AOB=∠COD,∴∠AOB-∠COB=∠COD-∠COB,即∠AOC=∠BOD;
(2)∵∠AOB+∠BOD=∠AOD
又∵∠AOB=90°,∠AOD=125°
∴∠BOD=35°
∵∠BOD+∠BOC=90°
∴∠BOC=55°;
(3)解:∠BOC与∠AOD互补.
当三角板AOB绕O点旋转时,这种互补关系没有变化,理由如下:
当∠BOC在∠AOD内部时
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC
=∠COD+∠AOB
=90°+90°=180°
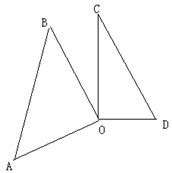
当∠BOC在∠AOD外部时,如下图
∠AOD+∠BOC=360°-∠AOB-∠COD=180°
∴∠BOC与∠AOD互补.
∵∠AOB=∠COD,∴∠AOB-∠COB=∠COD-∠COB,即∠AOC=∠BOD;
(2)∵∠AOB+∠BOD=∠AOD
又∵∠AOB=90°,∠AOD=125°
∴∠BOD=35°
∵∠BOD+∠BOC=90°
∴∠BOC=55°;

(3)解:∠BOC与∠AOD互补.
当三角板AOB绕O点旋转时,这种互补关系没有变化,理由如下:
当∠BOC在∠AOD内部时
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC
=∠COD+∠AOB
=90°+90°=180°
当∠BOC在∠AOD外部时,如下图
∠AOD+∠BOC=360°-∠AOB-∠COD=180°
∴∠BOC与∠AOD互补.

点评:①几何计算题中,如果依据题设和相关的几何图形的性质列出方程(或方程组)求解的方法叫做方程的思想;
②求角的度数常常要用到“三角形的内角和是180°这一隐含的条件;
③三角形的外角通常情况下是转化为内角来解决.
②求角的度数常常要用到“三角形的内角和是180°这一隐含的条件;
③三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
相关题目
 17、如图,将一副三角板的直角顶点重合,可得∠1=∠2,理由是等角
17、如图,将一副三角板的直角顶点重合,可得∠1=∠2,理由是等角 7、如图所示,将一副三角板的直角顶点重合摆放在桌面上,若∠AOD=145°,则∠BOC=
7、如图所示,将一副三角板的直角顶点重合摆放在桌面上,若∠AOD=145°,则∠BOC= 10、将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),下列结论一定成立的是( )
10、将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),下列结论一定成立的是( ) 4、如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC的度数为( )
4、如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠AOD=145°,则∠BOC的度数为( )