题目内容
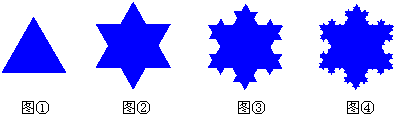
从一个等边三角形(如图①)开始,把它的各边分成相等的三段,再在各边中间一段上向外画出一个小等边三角形,形成六角星图形(如图②);然后在六角星各边上,用同样的方法向外画出更小的等边三角形,形成一个有18个尖角的图形(如图③);如果在其各边上,再用同样的方法向外画出更小的等边三角形(如图④).如此继续下去,图形的轮廓就能形成分支越来越多的曲线,这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线.
如果设原等边三角形边长为a,不妨把每一次的作图变化过程叫做“生长”,例如,第1次生长后,得图②,每个小等边三角形的边长为
a,所形成的图形的周长为4a.
请填写下表:(用含a的代数式表示)

如果设原等边三角形边长为a,不妨把每一次的作图变化过程叫做“生长”,例如,第1次生长后,得图②,每个小等边三角形的边长为
| 1 |
| 3 |
请填写下表:(用含a的代数式表示)
| 第1次 生长后 |
第2次 生长后 |
第3次 生长后 |
… | 第n次 生长后 | |||
| 每个小等边 三角形的边长 |
|
… | |||||
| 所形成的 图形的周长 |
4a | … |
分析:找到相邻两个图形的周长之间的关系:后一个图形在前一个的基础上多了它的
,以此类推,即可得到第4次变换后得到的图形的周长.边长变为原来的
.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:仔细观察规律发现:每生长一次,边长都变为原来的
,
即:第一次生长后,边长变为:
a;
第二次生长后,边长变为
×
a=
a;
第三次生长后,边长变为:
×
×
=
a
…
第三次生长后,边长变为:(
)na;
解:第一次生长后,周长:3a×
=4a
第二次生长后,周长:3a×
×
,
第三次生长后,周长:3a×
×
×
,
…
第n次生长后,周长:3a(
)n.
故答案为:
| 1 |
| 3 |
即:第一次生长后,边长变为:
| 1 |
| 3 |
第二次生长后,边长变为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
第三次生长后,边长变为:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
…
第三次生长后,边长变为:(
| 1 |
| 3 |
解:第一次生长后,周长:3a×
| 4 |
| 3 |
第二次生长后,周长:3a×
| 4 |
| 3 |
| 4 |
| 3 |
第三次生长后,周长:3a×
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
…
第n次生长后,周长:3a(
| 4 |
| 3 |
故答案为:
| 第1次 生长后 |
第2次 生长后 |
第3次 生长后 |
… | 第n次 生长后 | |||||||||
| 每个小等边 三角形的边长 |
|
|
|
… | (
| ||||||||
| 所形成的 图形的周长 |
4a | 3a(
|
3a(
|
… | 3a(
|
点评:本题主要考查了图形的变化类问题,找到后一个图形的周长是前一个图形周长的
,是解答本题的关键.
| 4 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从一个等边三角形(如图①)开始,把它的各边分成相等的三段,再在各边中间一段上向外画出一个小等边三角形,形成六角星图形(如图②);然后在六角星各边上,用同样的方法向外画出更小的等边三角形,形成一个有18个尖角的图形(如图③);如果在其各边上,再用同样的方法向外画出更小的等边三角形(如图④).如此继续下去,图形的轮廓就能形成分支越来越多的曲线,这就是瑞典数学家科赫将雪花理想化得到的科赫雪花曲线.

如果设原等边三角形边长为a,不妨把每一次的作图变化过程叫做“生长”,例如,第1次生长后,得图②,每个小等边三角形的边长为 ,所形成的图形的周长为4a.
,所形成的图形的周长为4a.
请填写下表:(用含a的代数式表示)
| 第1次 生长后 | 第2次 生长后 | 第3次 生长后 | … | 第n次 生长后 | |
| 每个小等边 三角形的边长 |  | ________ | ________ | … | ________ |
| 所形成的 图形的周长 | 4a | ________ | ________ | … | ________ |
 20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有
20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有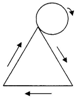 (2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
(2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了